题目内容
6.设{an}是等比数列,且a1=$\frac{3}{2}$,S3=$\frac{9}{2}$,则它的通项公式为an=( )| A. | $\frac{3}{2}$•($\frac{1}{2}$)n-1 | B. | $\frac{3}{2}•{({-\frac{1}{2}})^{n-2}}$ | C. | $\frac{3}{2}$•(-$\frac{1}{2}$)n-2 | D. | $\frac{3}{2}$•(-2)n-1或$\frac{3}{2}$ |
分析 由题意可得q的方程,解方程可得q,即可求出$\frac{3}{2}$•(-2)n-1或$\frac{3}{2}$.
解答 解:∵数列{an}为等比数列,且a1=$\frac{3}{2}$,S3=$\frac{9}{2}$,
∴S3=a1+a1q+a1q2=$\frac{3}{2}$(1+q+q2)=$\frac{9}{2}$,
整理可得q2+q-2=0,解得q=-2或q=1,
∴an=$\frac{3}{2}$•(-2)n-1或$\frac{3}{2}$,
故选:D.
点评 本题考查等比数列的通项、求和公式,属基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.已知集合A={x|x2-3x+2<0},B={x|y=lg(3-x)},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|x<3} |
14.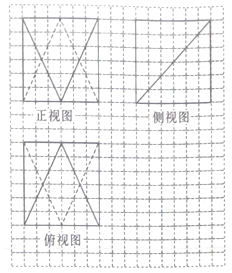 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )| A. | 72 | B. | $90\sqrt{3}$ | C. | $108\sqrt{2}$ | D. | 144 |
11.若a,b∈R,且a>b,则下列不等式中恒成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2>b2 | C. | 2a>2b | D. | $\frac{a}{b}>1$ |
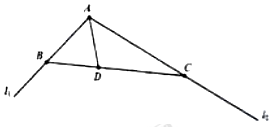 某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).
某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).