题目内容
抛物线C1: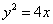 的焦点与椭圆C2:
的焦点与椭圆C2: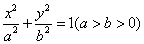 的一个焦点相同.设椭圆的右顶点为A,C1, C2在第一象限的交点为B,O为坐标原点,且
的一个焦点相同.设椭圆的右顶点为A,C1, C2在第一象限的交点为B,O为坐标原点,且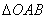 的面积为
的面积为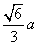 .
.
(1)求椭圆C2的标准方程;
(2)过A点作直线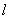 交C1于C,D两点,连接OC,OD分别交C2于E,F两点,记
交C1于C,D两点,连接OC,OD分别交C2于E,F两点,记 ,
,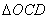 的面积分别为
的面积分别为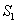 ,
,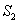 .问是否存在上述直线
.问是否存在上述直线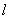 使得
使得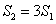 ,若存在,求直线
,若存在,求直线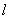 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
解:(1)∵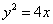 ∴焦点
∴焦点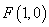 ∴
∴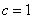 即
即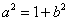
又∵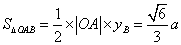 ∴
∴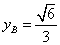
代入抛物线方程得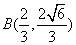 .又B点在椭圆上得
.又B点在椭圆上得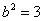 ,
,
∴椭圆C2的标准方程为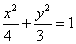 .
.
(2)设直线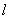 的方程为
的方程为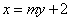 ,由
,由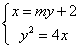 得
得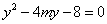
设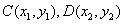 ,所以
,所以
又因为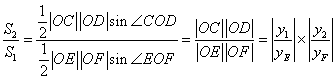
直线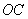 的斜率为
的斜率为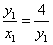 ,故直线
,故直线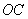 的方程为
的方程为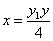 ,
,
由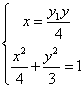 得
得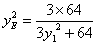 ,同理
,同理
所以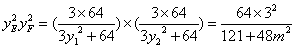
则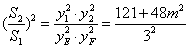 ,
,
所以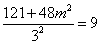 ,
,
所以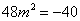 ,故不存在直线
,故不存在直线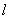 使得
使得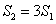

练习册系列答案
相关题目
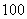 名年龄段在
名年龄段在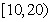 ,
,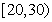 ,
, ,
, 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.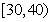 的人数;
的人数; 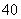 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取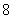 人,求
人,求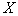 为年龄在
为年龄在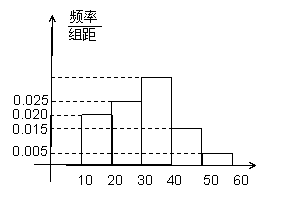
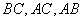 长分别为
长分别为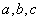 ,重心为G,则
,重心为G,则 =_______________;
=_______________; 中,椭
中,椭 圆
圆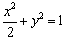 的左、右焦点分别为
的左、右焦点分别为 ,
, .设
.设 是椭圆上位于
是椭圆上位于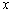 轴上方的两点,且直线
轴上方的两点,且直线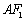 与直线
与直线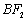 平行,
平行, 与
与 交于点P,且
交于点P,且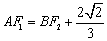 ,则直线
,则直线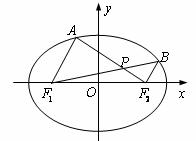
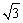 B.
B. 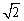 C.
C. 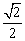 D. 1
D. 1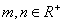 ,若直线
,若直线 与圆
与圆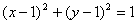 相切,则mn的取值范围是_____________
相切,则mn的取值范围是_____________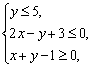 则
则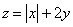 的最大值是( )
的最大值是( )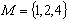 ,
, ,
,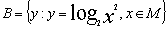 ,则集合
,则集合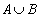 中元素有 个。
中元素有 个。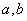 满足
满足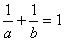 ,则
,则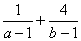 的最小值为( )
的最小值为( )