题目内容

15．若0＜x＜y＜1，则（　　）
A．3y＜3xB．log4x＜log4yC．（$\frac{1}{4}$）x＜（$\frac{1}{4}$）yD．logx3＜logy3

分析 根据指数函数和对数函数的单调性即可判断．

解答 解：根据指数函数单调性，y=ax，当a＞1时为增函数，当0＜a＜1，为减函数，
∵0＜x＜y＜1，
∴3x＜3y，$（\frac{1}{4}）^{x}$＞$（\frac{1}{4}）^{y}$，
根据对数函数单调性，y=logax，当a＞1时为增函数，当0＜a＜1，为减函数，
∴log4x＜log4y，logx3＞logy3，
故选：B．

点评 本题考查了指数函数和对数函数的单调性，属于基础题．

练习册系列答案
相关题目
2．若数列{an}是公比为q的等比数列，下列数列中不是等比数列的是（　　）
A．{an•an+1}B．{nan}C．{${a}_{n}^{2}$}D．$\frac{{a}_{n}}{{a}_{n+1}}$
3．已知函数f（x）=（2ax-x2）eax（a≥0）
（Ⅰ）若函数f（x）在区间$（\sqrt{2}，2）$上单调递减，求实数a的取值范围．
（Ⅱ）若函数f（x）在区间$（\sqrt{2}，2）$上存在单调递减区间，求实数a的取值范围．
3．汽车的最佳使用年限是使年均消耗费用最低的年限（年均消耗费用=年均成本费+年均维修费），设某种汽车的购车的总费用为50000元；使用中每年的保险费、养路费及汽油费合计为6000元；前x年的总维修费y满足y=ax2+bx，已知第一年的维修费为1000元，前二年总维修费为3000元，这这种汽车的最佳使用年限为（　　）
A．8B．9C．10D．12
10．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知$\frac{a}{sinA}=\frac{b}{{\sqrt{3}cosB}}$．
（Ⅰ）求角B的值；
（Ⅱ）求sinA+sinC的取值范围．
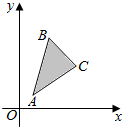20．给出平面区域如图所示，其中A（1，1），B（2，5），C（4，3）若使目标函数z=ax-y仅在点C处取得最大值，则a的取值范围是$（{\frac{2}{3}，+∞}）$．
7．已知△ABC中，角A，B，C所对的边分别为a，b，c，且满足$sinA（sinB+\sqrt{3}cosB）=\sqrt{3}sinC$．
（1）求角A的大小；    
（2）若$a=2\sqrt{3}，\;b+c=4$，求△ABC的面积．
4．已知函数$f（x）={log_a}（ax）•{log_a}（{a^2}x）$在x∈[2，8]时取得最大值2，最小值$-\frac{1}{4}$，求a．
5．设集合A={0，1，2，4}，B=$\left\{{\left.{x∈R|\frac{x-4}{x-2}≤0}\right\}}$，则A∩B=（　　）
A．{1，2，3，4}B．{2，3，4}C．{4}D．{x|1＜x≤4}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网