题目内容
已知双曲线上
-
=1(a>0,b>0)一点C,过双曲线中心的直线交双曲线于A,B两点,记直线AC,BC的斜率分别为k1,k2,当
+ln(k1k2)最小时,双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| k1k2 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:设A(x1,y1),C(x2,y2),由双曲线的对称性得B(-x1,-y1),从而得到k1k2=
•
=
,再由构造法利用导数性质能求出双曲线的离心率.
| y2-y1 |
| x2-x1 |
| y2+y1 |
| x2+x1 |
| y22-y12 |
| x22-x12 |
解答:
解:设A(x1,y1),C(x2,y2),
由题意知点A,B为过原点的直线与双曲线
-
=1的交点,
∴由双曲线的对称性得A,B关于原点对称,
∴B(-x1,-y1),
∴k1k2=
•
=
,
∵点A,C都在双曲线上,
∴
-
=1,
-
=1,
两式相减,可得:k1k2=
>0,
对于函数y=
+lnx(x>0),
由y′=-
+
=0,得x=0(舍)或x=2,
x>2时,y′>0,0<x<2时,y′<0,
∴当x=2时,函数y=
+lnx(x>0)取得最小值,
∴当
+ln(k1k2)最小时,k1k2=
=2,
∴e=
=
.
故答案为:
.
由题意知点A,B为过原点的直线与双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴由双曲线的对称性得A,B关于原点对称,
∴B(-x1,-y1),
∴k1k2=
| y2-y1 |
| x2-x1 |
| y2+y1 |
| x2+x1 |
| y22-y12 |
| x22-x12 |
∵点A,C都在双曲线上,
∴
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
两式相减,可得:k1k2=
| b2 |
| a2 |
对于函数y=
| 2 |
| x |
由y′=-
| 2 |
| x2 |
| 1 |
| x |
x>2时,y′>0,0<x<2时,y′<0,
∴当x=2时,函数y=
| 2 |
| x |
∴当
| 2 |
| k1k2 |
| a2 |
| b2 |
∴e=
1+
|
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的离心率的求法,涉及到导数、最值、双曲线、离心率等知识点,综合性强,难度大,解题时要注意构造法的合理运用.

练习册系列答案
相关题目
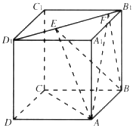 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=