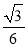题目内容
19.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,过F2与双曲线的一条渐近线平行的直线与另一条渐近线平行的直线与另一条渐近线交于点M,且cos∠F1MF2=0,则双曲线的离心率为$\sqrt{5}$.分析 先根据题意可表示出过焦点的直线与双曲线方程联立求得交点M的坐标,F1,F2的坐标,进而表示出$\overrightarrow{M{F}_{1}}$,$\overrightarrow{M{F}_{2}}$,进而根据cos∠F1MF2=0,即$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,求得a和b的关系,进而求得a和c的关系,离心率可得.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,F2(c,0),
依题意$\left\{\begin{array}{l}{{b}^{2}{x}^{2}-{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\\{y=\frac{b}{a}(x-c)}\end{array}\right.$,解得x=$\frac{{a}^{2}+{c}^{2}}{2c}$,y=-$\frac{{b}^{3}}{2ac}$,
即有M($\frac{{a}^{2}+{c}^{2}}{2c}$,-$\frac{{b}^{3}}{2ac}$),F1(-c,0),F2(c,0),
∴$\overrightarrow{M{F}_{1}}$=($\frac{-{a}^{2}-3{c}^{2}}{2c}$,$\frac{{b}^{3}}{2ac}$),$\overrightarrow{M{F}_{2}}$=($\frac{{b}^{2}}{2c}$,$\frac{{b}^{3}}{2ac}$),
∵cos∠F1MF2=0,即有$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,
即$\frac{-{a}^{2}-3{c}^{2}}{2c}$•$\frac{{b}^{2}}{2c}$+$\frac{{b}^{3}}{2ac}$•$\frac{{b}^{3}}{2ac}$=0,
∴c4=5a2c2,
∴e=$\frac{c}{a}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题主要考查了双曲线的简单性质,考查了学生综合分析问题和解决问题的能力.圆锥曲线是高考的重点每年必考,希望能够引起考生的重视.

 阅读快车系列答案
阅读快车系列答案| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
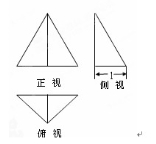
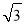 B.
B.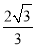 C.
C. D.
D.