题目内容
9.已知虚数$z=\frac{5}{3-4i}-\frac{4+3i}{5}$,则z的虚部是( )| A. | $-\frac{1}{5}$ | B. | $-\frac{1}{5}i$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}i$ |
分析 利用复数代数形式的乘除运算化简得答案.
解答 解:∵$z=\frac{5}{3-4i}-\frac{4+3i}{5}$=$\frac{5(3+4i)}{(3-4i)(3+4i)}-\frac{4}{5}-\frac{3i}{5}$=$\frac{3}{5}+\frac{4i}{5}-\frac{4}{5}-\frac{3i}{5}=-\frac{1}{5}+\frac{1}{5}i$,
∴z的虚部是$\frac{1}{5}$.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
17.设向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°,且$|{\overrightarrow a}|=2\sqrt{2},|{\overrightarrow b}|=\sqrt{3}$,则$\overrightarrow a•\overrightarrow b$等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | 6 |
14.$\frac{2}{1+i}-\frac{1+i}{2}$=( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{2}-\frac{1}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{1}{2}-\frac{3}{2}i$ |
19.如图为一个几何体的三视图,则该几何体外接球的表面积为( )


| A. | 4$\sqrt{3}$π | B. | 12π | C. | 12$\sqrt{3}$π | D. | 24π |
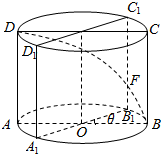 如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.
如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.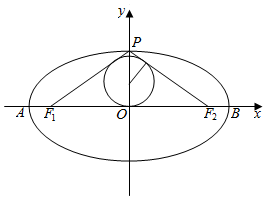 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$