题目内容
8.已知椭圆C的中心在原点,对称轴为坐标轴,右焦点为F(2,0),离心率为$\frac{\sqrt{2}}{2}$.(1)求椭圆C的方程;
(2)过点F且不垂直于坐标轴的直线l交椭圆C于不同的两点M,N,线段MN的垂直平分线与x轴交于点D,求点D的横坐标的取值范围.
分析 (1)由题意知,c=2,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,从而求椭圆的方程;
(2)设直线l的方程为y=k(x-2),从而联立方程化简得(1+2k2)x2-8k2x+8k2-8=0,从而结合韦达定理得x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-8}{2{k}^{2}+1}$;从而求得.
解答 解:(1)由题意知,
c=2,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故a=$2\sqrt{2}$,b=2,
故椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)设直线l的方程为y=k(x-2),k为斜率且k≠0,
设M(x1,y1),N(x2,y2),
将其代入$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,
整理得(1+2k2)x2-8k2x+8k2-8=0,
由于F在椭圆内,当然对任意实数都有△>0;
根据韦达定理得,
x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-8}{2{k}^{2}+1}$;
y1+y2=k(x1-2)+k(x2-2)=k(x1+x2)-4k=$\frac{-4k}{2{k}^{2}+1}$,
于是线段MN的中点为($\frac{4{k}^{2}}{2{k}^{2}+1}$,$\frac{-2k}{2{k}^{2}+1}$),
则线段MN的垂直平分线方程为y-$\frac{-2k}{2{k}^{2}+1}$=-$\frac{1}{k}$(x-$\frac{4{k}^{2}}{2{k}^{2}+1}$).
令y=0,得x=$\frac{2{k}^{2}}{2{k}^{2}+1}$=1-$\frac{1}{2{k}^{2}+1}$,
1+2k2∈(1,+∞),
所以点D横坐标的取值范围是(0,1).
点评 本题考查了圆锥曲线与直线的位置关系的应用及学生的化简运算能力的应用.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$ | C. | $\frac{{x}^{2}}{5}+\frac{{y}^{2}}{3}=1$ | D. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ |
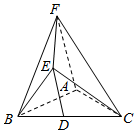 在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.
在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.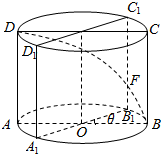 如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.
如图所示,已知圆柱OO1的底面半径是2,高是4,ABCD是圆柱的一个轴截面,动点E从B点出发,沿着圆柱的侧面到达点D,当其经过的路程最短时,在侧面留下的曲线是S,将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1和曲线S交于点F.