题目内容
边长为a的正四面体的内切球半径为 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:作AO1⊥平面BCD于O1,则O1为△BCD的中心,求BO1=
×
a=
a,AO1=
=
a,在平面ABO1内作AB的垂直平分线交AO1于O,O是内切球球心,由此能求出正四面体的内切球半径.
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
a2-(
|
| ||
| 3 |
解答:
解:如图设ABCD是棱长为a的正四面体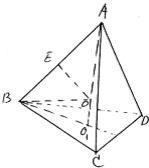
作AO1⊥平面BCD于O1,则O1为△BCD的中心
则BO1=
×
a=
a,
∴AO1=
=
a,
在平面ABO1内作AB的垂直平分线交AO1于O,则AO=BO=CO=DO,
且O到平面BCD、ABC、ACD、ABD的距离相等,
∴O是正四面体的内切球,外接球球心
∵
=
,∴AO=
=
a,
∴正四面体的内切球半径为:OO1=
a-
a=
a.
故答案为:
a.

作AO1⊥平面BCD于O1,则O1为△BCD的中心
则BO1=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴AO1=
a2-(
|
| ||
| 3 |
在平面ABO1内作AB的垂直平分线交AO1于O,则AO=BO=CO=DO,
且O到平面BCD、ABC、ACD、ABD的距离相等,
∴O是正四面体的内切球,外接球球心
∵
| AO |
| AB |
| AE |
| AO1 |
| ||||
|
| ||
| 4 |
∴正四面体的内切球半径为:OO1=
| ||
| 3 |
| ||
| 4 |
| ||
| 12 |
故答案为:
| ||
| 12 |
点评:本题考查正四面体的内切球半径的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
在△ABC中,若
=
,则C的值为( )
| sinA |
| a |
| cosC |
| c |
| A、30° | B、45° |
| C、60° | D、90° |
