题目内容
将函数f(x)=2sin(x-
)cos(x-
)+
cos2(x-
)在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N+).
(1)求数列{an}的通项公式;
(2)若an=
,求数列{bn}的前n项和Tn.
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
(1)求数列{an}的通项公式;
(2)若an=
| bn |
| 2n |
考点:数列的求和,三角函数中的恒等变换应用
专题:等差数列与等比数列
分析:(1)f(x)=2sin2x,由正弦函数的性质,其极值点为x=
π+
,由此能求出数列{an}的通项公式.
(2)bn=2n•an=
•(2n-1)•2n,由此利用错位相减法能求出数列{bn}的前n项和Tn.
| k |
| 2 |
| π |
| 4 |
(2)bn=2n•an=
| π |
| 4 |
解答:
解:(1)f(x)=2sin(x-
)cos(x-
)+
cos2(x-
)
=sin(2x-
)+
cos(2x-
)
=2sin2x,
由正弦函数的性质,其极值点为x=
π+
,
它在(0,+∞)内的全部极值点构成以
为首项,
为公差的等差数列,
数列{an}的通项公式为an=
+(n-1)•
=
π,(n∈N*).
(2)∵an=
,∴bn=2n•an=
•(2n-1)•2n,
∴Tn=
[1•2+3•22+…+(2n-1)•2n],①
2Tn=
[1•22+3•23+…+(2n-1)•2n+1],②
①-②,得:-Tn=
[2+23+24+…+2n+1-(2n-1)•2n+1]
=
[2+
-(2n-1)•2n+1]
=
[-6+(3-2n)•2n+1],
∴Tn=
[3-(3-2n)•2n].
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
=sin(2x-
| π |
| 3 |
| 3 |
| π |
| 3 |
=2sin2x,
由正弦函数的性质,其极值点为x=
| k |
| 2 |
| π |
| 4 |
它在(0,+∞)内的全部极值点构成以
| π |
| 4 |
| π |
| 2 |
数列{an}的通项公式为an=
| π |
| 4 |
| π |
| 2 |
| 2n-1 |
| 4 |
(2)∵an=
| bn |
| 2n |
| π |
| 4 |
∴Tn=
| π |
| 4 |
2Tn=
| π |
| 4 |
①-②,得:-Tn=
| π |
| 4 |
=
| π |
| 4 |
| 8(1-2n-1) |
| 1-2 |
=
| π |
| 4 |
∴Tn=
| π |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
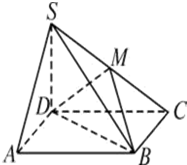 如图四棱锥S-ABCD,底面ABCD是正方形,SD⊥底面ABCD,M为SC的中点.
如图四棱锥S-ABCD,底面ABCD是正方形,SD⊥底面ABCD,M为SC的中点.