题目内容
函数 .
.
(1)若 ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;
(2)设 ,若对任意
,若对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)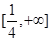 ;(2)
;(2)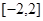 .
.
解析试题分析:(1)由题意可得,当 时,
时, 在区间
在区间 上是单调递增函数等价于对于任意的
上是单调递增函数等价于对于任意的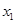 ,
, (不妨
(不妨 ),
),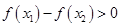 恒成立,从而将问题转化为
恒成立,从而将问题转化为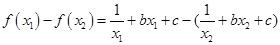
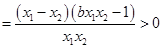 在
在 恒成立,即有
恒成立,即有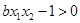 ,
,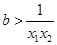 在
在 上恒成立,而的
上恒成立,而的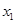 ,
, ,且
,且 ,故有
,故有 ,因此分析可得要使
,因此分析可得要使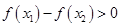 恒成立,只需
恒成立,只需 ,即有实数
,即有实数 的取值范围是
的取值范围是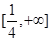 ;(2)由题意分析可得问题等价于在
;(2)由题意分析可得问题等价于在 上,
上,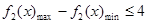 ,从而可将问题转化为在
,从而可将问题转化为在 上,求二次函数
上,求二次函数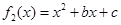 的最大值与最小值,因此需要对二次函数的对称轴
的最大值与最小值,因此需要对二次函数的对称轴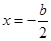 分以下四种情况讨论:①当
分以下四种情况讨论:①当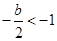 ,即
,即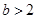 ;②当
;②当 ,即
,即 ;③当
;③当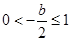 ,即
,即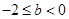 ;④当
;④当 ,即
,即 ,结合二次函数的图像和性质,可分别得到
,结合二次函数的图像和性质,可分别得到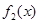 在以上四种情况下的最大值与最小值,从而可得实数
在以上四种情况下的最大值与最小值,从而可得实数 的取值范围是
的取值范围是 .
.
试题解析:(1) 时,
时,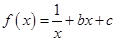 ,
,
任设 ,
,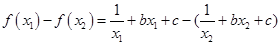
 , ..2分
, ..2分 ,
,
∵函数 在
在 上是单调递增函数,∴恒有
上是单调递增函数,∴恒有 ,..........3分
,..........3分
∴恒有 ,即恒有
,即恒有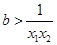 , .4分
, .4分
当 时,
时, ,∴
,∴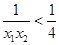 ,∴
,∴ ,即实数
,即实数 的取值范围是
的取值范围是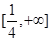 ..6分
..6分
(2)当 时
时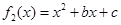 ,
,
对任意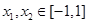 有
有 恒成立等价于
恒成立等价于 在
在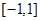 上的最大值与最小值之差
上的最大值与最小值之差 ..7分
..7分
当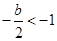 ,即
,即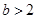 时,
时, 在
在 上单调递增,
上单调递增,
∴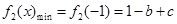 ,
, ,∴
,∴ ,与题设矛盾; ..9分
,与题设矛盾; ..9分
当 ,即
,即
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

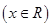 满足
满足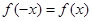 ,
,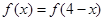 ,且当
,且当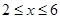 时,
时,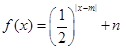 .
.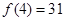 ,求
,求 的值.
的值.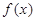 是定义在
是定义在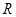 上的奇函数,当
上的奇函数,当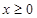 时,
时, .
. ;
;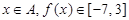 ,求区间
,求区间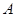 .
. 有最小正周期2,且当
有最小正周期2,且当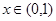 时,
时, .
.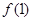 和
和 的值;
的值;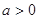 且
且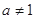 ,函数
,函数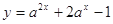 在
在 的最大值是14,求
的最大值是14,求 的值。
的值。 及二次函数
及二次函数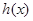 满足:
满足: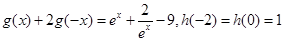 且
且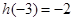 .
.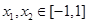 ,均有
,均有 成立,求
成立,求 的取值范围;
的取值范围; ,讨论方程
,讨论方程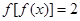 的解的个数情况.
的解的个数情况.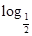 24)的值.
24)的值. 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且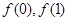 均为奇数.求证:
均为奇数.求证: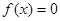 无整数根。
无整数根。 是奇函数,则a= .
是奇函数,则a= .