题目内容
已知函数
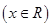 满足
满足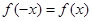 ,
,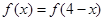 ,且当
,且当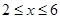 时,
时,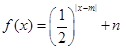 .
.
(1)证明:函数 是周期函数;(2)若
是周期函数;(2)若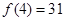 ,求
,求 的值.
的值.
(1)证明略;(2) .
.
解析试题分析:(1)对应函数 ,如果存在一个非零常数
,如果存在一个非零常数 ,使得当
,使得当 取定义域内的每一个值时,都有
取定义域内的每一个值时,都有 ,那么
,那么 为这个函数的周期;(2)函数
为这个函数的周期;(2)函数 在定义域上满足
在定义域上满足 ,则
,则 的周期为
的周期为 的周期函数;(3)进行指数幂的运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序,需注意下列问题:一是对于含有字母的化简求值的结果,一般用分数指数幂来表示,二是应用平方差、完全平方公式及
的周期函数;(3)进行指数幂的运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序,需注意下列问题:一是对于含有字母的化简求值的结果,一般用分数指数幂来表示,二是应用平方差、完全平方公式及 简化运算.
简化运算.
试题解析:(1)∵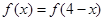 ,∴
,∴ ,又∵
,又∵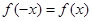 ,
,
∴ ,函数
,函数 是以4为周期的周期函数; 6分
是以4为周期的周期函数; 6分
(2)由(1)可知 ,∴
,∴
∴ ,从而
,从而 ,∴
,∴ ,又
,又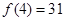 ,
,
∴ ,∴
,∴ . 12分
. 12分
考点:函数的周期性;(2)指数幂的运算.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
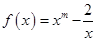 且
且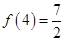 ,
, 的值;
的值;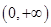 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.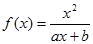 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4. 的值域.
的值域. ,当
,当 时,恒有
时,恒有 .
. 为正实数,
为正实数, ,并且
,并且 ,试求
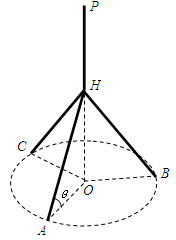
,试求 构成,其底端三点
构成,其底端三点 均匀地固定在半径为
均匀地固定在半径为 的圆
的圆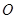 上(圆
上(圆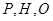 三点相异且共线,
三点相异且共线,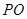 与地面垂直. 现要求点
与地面垂直. 现要求点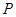 到地面的距离恰为
到地面的距离恰为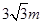 ,记用料总长为
,记用料总长为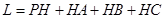 ,设
,设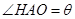 .
.
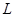 表示为
表示为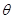 的函数,并注明定义域;
的函数,并注明定义域; .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围; ,若对任意
,若对任意 恒成立,求
恒成立,求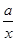 (x≠0,a∈R).
(x≠0,a∈R). 且
且 ,则
,则