题目内容
定义在R上的函数 及二次函数
及二次函数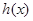 满足:
满足: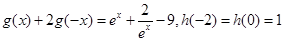 且
且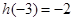 .
.
(1)求 和
和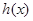 的解析式;
的解析式;
(2)对于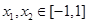 ,均有
,均有 成立,求
成立,求 的取值范围;
的取值范围;
(3)设 ,讨论方程
,讨论方程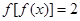 的解的个数情况.
的解的个数情况.
(1)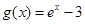 ,
,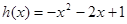 ;(2)
;(2) 的取值范围为
的取值范围为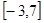 ;(3)
;(3)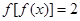 有5个解.
有5个解.
解析试题分析:(1)根据已知的函数方程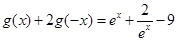 ,可以得到
,可以得到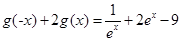 ,联立已知条件的函数方程,即可解得
,联立已知条件的函数方程,即可解得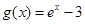 ,又由条件二次函数
,又由条件二次函数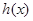 及
及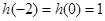 ,可设
,可设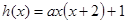 ,再根据
,再根据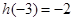 ,可求得
,可求得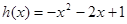 ;(2)问题等价于求使
;(2)问题等价于求使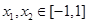 ,
, 恒成立的
恒成立的 的取值范围,即求当
的取值范围,即求当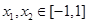 ,
,
使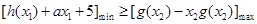 成立的
成立的 的取值范围,通过判断
的取值范围,通过判断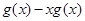 的单调性可知,其在
的单调性可知,其在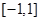 上单调递增,因此只需
上单调递增,因此只需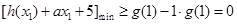 ,由(1)求得的二次函数
,由(1)求得的二次函数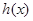 的解析式,可得只需
的解析式,可得只需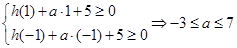 ,即
,即 的取值范围为
的取值范围为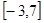 ;(3)根据条件及(1),(2)所求得的解析式,可画出
;(3)根据条件及(1),(2)所求得的解析式,可画出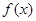 的示意图,根据示意图,可以得到方程
的示意图,根据示意图,可以得到方程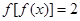 即等价于
即等价于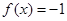 或
或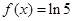 ,再从
,再从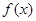 示意图上可得:
示意图上可得: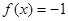 有2个解,
有2个解, 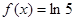 有
有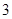 个解,因此
个解,因此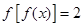 有
有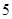 个解.
个解.
试题解析:(1) 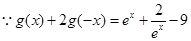 ,①
,①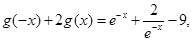 即
即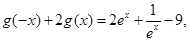 ②
②
由①②联立解得: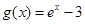 . 2分,
. 2分,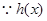 是二次函数, 且
是二次函数, 且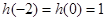 ,可设
,可设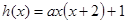 ,
,
由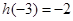 ,解得
,解得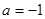 .∴
.∴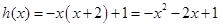 ,
,
∴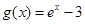 ,
,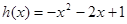 5分;
5分;
(2)设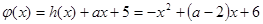 ,
, ,
,
依题意知:当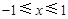 时,
时, 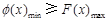
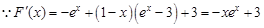 ,在
,在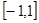 上单调递减,
上单调递减,
∴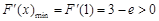 7分
7分
∴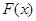 在
在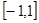 上单调递增,,∴
上单调递增,,∴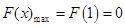
∴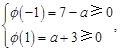 解得:
解得: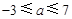 ,
,
∴实数 的取值范围为
的取值范围为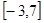 . 10分;
. 10分;
由题意,可画出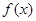 的示意图如图所示:
的示意图如图所示: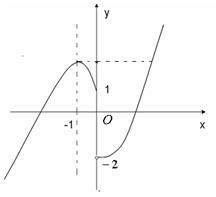
令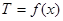 ,则
,则

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
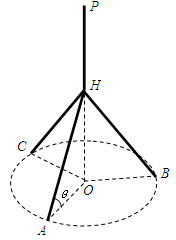
 构成,其底端三点
构成,其底端三点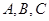 均匀地固定在半径为
均匀地固定在半径为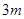 的圆
的圆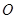 上(圆
上(圆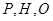 三点相异且共线,
三点相异且共线,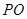 与地面垂直. 现要求点
与地面垂直. 现要求点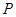 到地面的距离恰为
到地面的距离恰为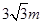 ,记用料总长为
,记用料总长为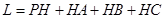 ,设
,设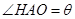 .
.
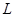 表示为
表示为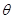 的函数,并注明定义域;
的函数,并注明定义域; .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围; ,若对任意
,若对任意 恒成立,求
恒成立,求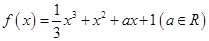 .
.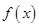 的单调区间;
的单调区间;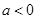 时,试讨论是否存在
时,试讨论是否存在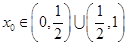 ,使得
,使得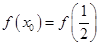 .
.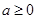 ,函数
,函数
 =4,求函数
=4,求函数 的反函数
的反函数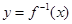 ;
;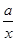 (x≠0,a∈R).
(x≠0,a∈R). .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 的二阶周期点.证明函数
的二阶周期点.证明函数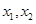 ;
;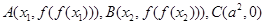 ,记
,记 的面积为
的面积为 ,求
,求 上的最大值和最小值。
上的最大值和最小值。