题目内容
若等差数列{an}的前n项和公式为Sn=pn2+（p+1）n+p+3，则p= ，首项a1= ，公差d= ．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由题意可表示出数列的前三项，由2a2=a1+a3可得p值，进而可得首项和公差．
解答：
解：由题意可得a1=S1=p+（p+1）+p+3=3p+4，
a2=S2-S1=4p+1，a3=S3-S2=6p+1，
由2a2=a1+a3可得2（4p+1）=3p+4+6p+1，
解得p=-3，∴a1=3p+4=-5，a2=4p+1=-11，
∴公差d=a2-a1=-6
故答案为：-3；-5；-6
a2=S2-S1=4p+1，a3=S3-S2=6p+1，
由2a2=a1+a3可得2（4p+1）=3p+4+6p+1，
解得p=-3，∴a1=3p+4=-5，a2=4p+1=-11，
∴公差d=a2-a1=-6
故答案为：-3；-5；-6
点评：本题考查等差数列的求和公式和通项公式，属基础题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
sin（-
）的值是（ ）
| 13π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设P、Q是函数f（x）=2sin（2x+φ）（φ为常数）图象上的两点且横坐标分别为-
、
，若f（x）图象上存在一个最高点M，使得（
+
）•
=0，则下列关系一定成立的是 （ ）
| π |
| 12 |
| π |
| 4 |
| MP |
| MQ |
| PQ |
A、f（
| ||||
B、f（
| ||||
C、f（
| ||||
D、f（-
|
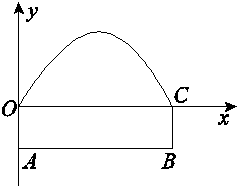有一条双向公路隧道，其横断面由抛物线和矩形ABCO的三边组成，隧道的最大高度为4.9m，AB=10m，BC=2.4m．现把隧道的横断面放在平面直角坐标系中，若有一辆高为4m，宽为2m的装有集装箱的汽车要通过隧道．问：如果不考虑其他因素，汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部（抛物线部分为隧道顶部，AO、BC为壁）？