题目内容
在平面直角坐标系xOy中，A（1，0），B（2，0）是两个定点，曲线C的参数方程为
（θ为参数）．
（Ⅰ）将曲线C的参数方程化为普通方程；
（Ⅱ）以A（1，0）为极点，|
|为长度单位，射线AB为极轴建立极坐标系，求曲线C的极坐标方程．[来．
|
（Ⅰ）将曲线C的参数方程化为普通方程；
（Ⅱ）以A（1，0）为极点，|
| AB |
考点：简单曲线的极坐标方程,参数方程化成普通方程
专题：坐标系和参数方程
分析：（I）利用cos2θ+sin2θ=1可得可把曲线C的参数方程
（θ为参数）消去参数化为直角坐标方程；
（II）由建立极坐标系的方法可得曲线C的极坐标方程为ρ=2cosθ．
|
（II）由建立极坐标系的方法可得曲线C的极坐标方程为ρ=2cosθ．
解答：
解：（I）曲线C的参数方程
（θ为参数）消去参数可得（x-2）2+y2=1．
（II）以A（1，0）为极点，|
|为长度单位，射线AB为极轴建立极坐标系，则曲线C的极坐标方程为ρ=2cosθ．
|
（II）以A（1，0）为极点，|
| AB |
点评：本题考查了把参数方程化为直角坐标方程、直角坐标化为极坐标方程，属于基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
如果扇形圆心角的弧度数为2，圆心角所对的弦长也为2，那么这个扇形的面积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设M={0，1，2，4，5，8}，N={0，2，3，5}，则N∩M=（ ）
| A、{1，3} |
| B、{1，4，8} |
| C、{0，2，5} |
| D、{2，4，6} |
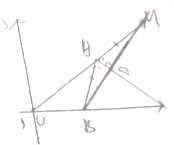如图，△ABC的周长为8，C（0，0），B（2，0），过B的直线与∠CAB的外角平分线垂直，且交AC的延长线于M，求点M的轨迹方程．
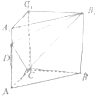如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，四边形BCC1B1是边长为4的正方形，直线AB与平面ACC1A1所成角的正切值为2，点D为棱AA1上的动点．
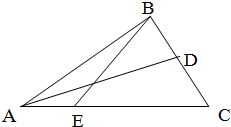如图，在△ABC中，D是BC的中点，E是AC的三等分点，且EC=2AE，若