题目内容
已知函数f（x）满足f（-x）=f（x）和f（x+2）=f（x），且当x∈[0，1]时，f（x）=1-x，则关于x的方程f（x）=（
）x在x∈[0，4]上解的个数是（ ）
| 1 |
| 3 |
| A、5 | B、4 | C、3 | D、2 |
考点：函数的周期性,函数奇偶性的性质
专题：函数的性质及应用
分析：由题意可得，函数f（x）为偶函数，且是周期为2的周期函数，本题即求函数y=f（x）的图象与函数y=（
）x的图象在[0，4]上的交点个数，数形结合可得结论．
| 1 |
| 3 |
解答：
解：由题意可得，函数f（x）为偶函数，且是周期为2的周期函数．
方程f（x）=（
）x在x∈[0，4]上解的个数，
即函数y=f（x）的图象与函数y=（
）x的图象在[0，4]上的交点个数，
再根据当x∈[0，1]时，f（x）=1-x，
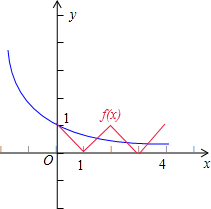
画出函数f（x）在[0，4]上的图象，数形结合可得，
函数y=f（x）的图象与函数y=（
）x的图象在[0，4]上的交点个数为4，
故选：B．
解：由题意可得，函数f（x）为偶函数，且是周期为2的周期函数．方程f（x）=（
| 1 |
| 3 |
即函数y=f（x）的图象与函数y=（
| 1 |
| 3 |
再根据当x∈[0，1]时，f（x）=1-x，
画出函数f（x）在[0，4]上的图象，数形结合可得，
函数y=f（x）的图象与函数y=（
| 1 |
| 3 |
故选：B．
点评：本题主要考查函数的单调性、奇偶性的应用，函数零点与方程的根的关系，体现了转化以及数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
将一根长为3m的木棒随机折成三段，折成的这三段木棒能够围成三角形的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线y=x+m与圆x2+y2+4x+2=0有两个不同的公共点，则实数m的取值范围是（ ）
| A、（0，4） | ||||
| B、（-4，0） | ||||
C、(-2-
| ||||
D、(2-
|