题目内容
16.如果(1+x)n的展开式中x2的系数等于x的系数的3倍,则n的值为7.分析 根据二项式(1+x)n展开式的通项,结合题意列出方程求出n的值即可.
解答 解:二项式(1+x)n展开式的通项为
Tr+1=${C}_{n}^{r}$•xr,
由x2项的系数等于x项的系数的3倍,
可得${C}_{n}^{2}$=3${C}_{n}^{1}$,
即$\frac{1}{2}$n(n-1)=3n,
解得n=7或n=0(不合题意,舍去).
故答案为:7.
点评 本题考查了二项式定理的通项公式及运用问题,也考查了运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.把函数y=sinx(x∈R)的图象上所有的点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再把所得图象向左平行移动$\frac{π}{6}$个单位长度,得到的图象所表示的函数是( )
| A. | y=sin($\frac{1}{2}$x+$\frac{π}{6}}$),x∈R | B. | y=sin($\frac{1}{2}$x+$\frac{π}{12}$),x∈R | ||
| C. | y=sin(2x+$\frac{π}{3}$),x∈R | D. | y=sin(2x+$\frac{π}{6}$),x∈R |
1.函数f(x)=ln(x2+2)-ex-1的图象可能是( )
| A. |  | B. | 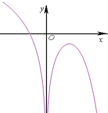 | C. | 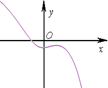 | D. |  |