题目内容
已知函数f(x)=Acos(ωx+θ)的图象如图所示,f(
)=-
,则f(-
)=( )
| π |
| 2 |
| 2 |
| 3 |
| π |
| 6 |

A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:根据条件根据图象求出函数的周期,根据三角函数的诱导公式,即可得到结论.
解答:
解:由题意可知,此函数的周期T=2(
-
)=
π,
故
=
π,
解得ω=3,
则f(x)=Acos(3x+φ).
f(
)=-
,
即f(
)=Acos(
+φ)=Asinφ=-
.
∴f(-
)=Acos[3×(-
)x+φ]=Acos(φ-
)=Asinφ=-
.
故选:A.
| 11π |
| 12 |
| 7π |
| 12 |
| 2 |
| 3 |
故
| 2π |
| ω |
| 2 |
| 3 |
解得ω=3,
则f(x)=Acos(3x+φ).
f(
| π |
| 2 |
| 2 |
| 3 |
即f(
| π |
| 2 |
| 3π |
| 2 |
| 2 |
| 3 |
∴f(-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 2 |
| 3 |
故选:A.
点评:本题主要考查三角函数的图象和性质,根据条件求出函数的周期以及利用诱导公式进行转化是解决本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下列函数在[
,π]上是增函数的是( )
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=cos2x |
| D、y=sin2x |
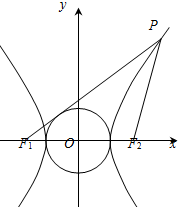 已知双曲线
已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=sin(x+φ)在区间(
,
)上单调递增,常数φ的值可能是( )
| π |
| 3 |
| 2π |
| 3 |
| A、0 | ||
B、
| ||
| C、π | ||
D、
|
执行如图所示的程序框图,则输出的结果为( )


| A、-2 | B、-1 | C、1 | D、2 |
已知变量x,y满足约束条件
,则z=3x+y的取值范围为( )
|
| A、[-1,1] |
| B、[-1,3] |
| C、[3,11] |
| D、[3,+∞) |