题目内容
设复数z1,z2在复平面内对应的点关于原点对称,z1=1+i,则z1z2=( )
| A、-2i | B、2i | C、-2 | D、2 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:通过复数的几何意义先得出z2,再利用复数的代数运算法则进行计算.
解答:
解:z1=1+i在复平面内的对应点为(1,1),
它关于原点对称的点为(-1,-1),
故z2=-1-i,
∴z1z2=-(1+i)2=-2i.
故选:A.
它关于原点对称的点为(-1,-1),
故z2=-1-i,
∴z1z2=-(1+i)2=-2i.
故选:A.
点评:本题复数的运算法则、几何意义,属于基础题.

练习册系列答案
相关题目
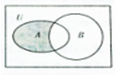
设全集U=R,A={x||x-1|<1},B={x|y=
},则图中阴影部分表示的集合是( )
| 1 | ||
|

| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1≤1} |