题目内容
已知c＞a＞b＞0，求证：
＞
．
| a |
| c+b |
| b |
| c+a |
考点：不等式的证明
专题：证明题
分析：利用分析法，依题意，要证明
＞
，只需证明a（c+a）＞b（b+c），整理易证该式成立，从而可得原式成立．
| a |
| c+b |
| b |
| c+a |
解答：
解：∵c＞a＞b＞0，
∴要证明
＞
，
只需证明a（c+a）＞b（b+c），
即证a2-b2+ac-bc=（a+b）（a-b）+c（a-b）=（a-b）（a+b+c）＞0，
∵c＞a＞b＞0，
∴a-b＞0，a+b+c＞0，
∴（a-b）（a+b+c）＞0，成立；
∴原不等式成立，即
＞
．
∴要证明
| a |
| c+b |
| b |
| c+a |
只需证明a（c+a）＞b（b+c），
即证a2-b2+ac-bc=（a+b）（a-b）+c（a-b）=（a-b）（a+b+c）＞0，
∵c＞a＞b＞0，
∴a-b＞0，a+b+c＞0，
∴（a-b）（a+b+c）＞0，成立；
∴原不等式成立，即
| a |
| c+b |
| b |
| c+a |
点评：本题考题不等式的证明，着重考查分析法的应用，考查推理能力，属于中档题．
练习册系列答案
相关题目
等比数列{an}的前n项和为Sn，已知S1，2S2，3S3成等差数列，则数列{an}的公比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
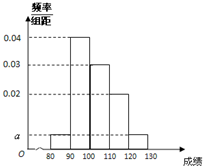为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]