题目内容
设0≤θ＜2π，已知两个向量
=(cosθ，sinθ)，
=(2+sinθ，2-cosθ)，则向量
长度的最大值是（ ）
| OP1 |
| OP2 |
| P1P2 |
A、
| ||
B、
| ||
C、3
| ||
D、2
|
分析：根据向量的减法法则求出
的坐标，利用向量模的坐标公式和同角平方关系，化简向量
的模代数式，再根据已知角的范围和余弦函数性质，求出
模的最大值．
| P1P2 |
| P1P2 |
| P1P2 |
解答：解：由向量的减法知，
=
-
=（2+sinθ-cosθ，2-cosθ-sinθ），
∴|
|=
=
=
，
∵0≤θ＜2π，∴-1≤cosθ≤1，
则当cosθ=-1时，
的长度有最大值是3
．
故选C．
| P1P2 |
| OP2 |
| OP1 |
∴|
| P1P2 |
| (2+sinθ-cosθ)2+(2-cosθ-sinθ)2 |
=
| 4+4(sinθ-cosθ)+(sinθ-cosθ)2+4-4(sinθ+cosθ)+(cosθ+sinθ)2 |
=
| 10-8cosθ |
∵0≤θ＜2π，∴-1≤cosθ≤1，
则当cosθ=-1时，
| P1P2 |
| 2 |
故选C．
点评：本题考查了向量减法和向量模的坐标运算，利用了同角的平方关系和余弦函数的性质，考查了运用知识和解决问题的能力．
练习册系列答案
相关题目
设0＜θ＜
，已知a1=2cosθ，an+1=
（n∈N*），猜想an等于（ ）
| π |
| 2 |
| 2+an |
A、2cos
| ||
B、2cos
| ||
C、2cos
| ||
D、2sin
|
，n∈N*，其中常数α，β均为非零实数，且α＋β≠0.
， a1＝1，a2＝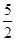
，求证：数列{| an＋1－an－1|}
(n∈N*，n≥2)与数列{n＋
} (n∈N*)中没有相同数值的项.