Question

设非常数数列{a_n}满足a_n+2＝，n∈N*，其中常数α，β均为非零实数，且α＋β≠0.

（1）证明：数列{a_n}为等差数列的充要条件是α＋2β＝0；

（2）已知α＝1，β＝， a₁＝1，a₂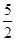＝，求证：数列{| a_n＋1－a_n－1|} (n∈N*，n≥2)与数列{n＋} (n∈N*)中没有相同数值的项.

 

Answer 1

【答案】

（1）等差数列的定义的运用，主要是根据相邻两项的差为定值来证明即可。

（2）由已知得，可知数列(n∈N*)为等比数列，进而得到，然后结合指数函数性质来得到。

【解析】

试题分析：（1）解：已知数列，.

①充分性：若，则有，得

，所以为等差数列.                       4分

②必要性：若为非常数等差数列，可令(k≠0). 代入

，得.

化简得，即.                          

因此，数列{a_n}为等差数列的充要条件是α＋2β＝0.                     8分

（2）由已知得.                               10分

又因为，可知数列(n∈N*)为等比数列，所以 (n∈N*).

从而有n≥2时， ，.

于是由上述两式，得 （）.                12分

由指数函数的单调性可知，对于任意n≥2，| a_n＋1－a_n－1|＝·≤·＝.

所以，数列中项均小于等于.

而对于任意的n≥1时，n＋≥1＋＞，所以数列{n＋}(n∈N*)中项均大于.

因此，数列与数列{n＋}(n∈N*)中没有相同数值的项.

16分

考点：等差数列，等比数列

点评：解决的关键是对于概念的准确运用，以及利用函数的性质来证明数列之间的关系。属于中档题。