题目内容
18.已知圆C:x2+y2-6x-8y+20=0,过原点O作圆C的两条切线,切点分别设为P,Q,(1)求切线的方程;
(2)求线段PQ的长.
分析 (1)求出圆心坐标和半径,利用点C到切线的距离为d=$\frac{{|{3k-4}|}}{{\sqrt{{k^2}+1}}}=\sqrt{5}$,求出k,即可求切线的方程;
(2)直角三角形中使用边角关系求出cosα,二倍角公式求出cos∠PO1Q,三角形PO1Q中,用余弦定理求出|PQ|.
解答 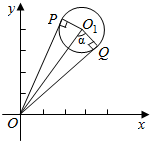 解:(1)由已知得圆的方程为:(x-3)2+(y-4)2=5,圆心C(3,4),
解:(1)由已知得圆的方程为:(x-3)2+(y-4)2=5,圆心C(3,4),
设切线:y=kx,即kx-y=0,点C到切线的距离为d=$\frac{{|{3k-4}|}}{{\sqrt{{k^2}+1}}}=\sqrt{5}$,
化简得4k2-24k+11=0,解得$k=\frac{11}{2},k=\frac{1}{2}$,
∴切线的方程为y=$\frac{11}{2}$x或y=$\frac{1}{2}$x;
(2)圆x2+y2-6x-8y+20=0 可化为 (x-3)2+(y-4)2 =5,
圆心(3,4)到原点的距离为5.故cosα=$\frac{\sqrt{5}}{5}$,
∴cos∠PO1Q=2cos2α-1=-$\frac{3}{5}$,
∴|PQ|2=($\sqrt{5}$)2+($\sqrt{5}$)2+2×($\sqrt{5}$)2×$\frac{3}{5}$=16.∴|PQ|=4
点评 本题考查直线与圆的位置关系,考查直角三角形中的边角关系,二倍角的余弦公式,以及用余弦定理求边长.

练习册系列答案
相关题目
13.已知a,b,c满足a<b<c且ac<0,则下列选项中一定成立的是( )
| A. | ab<ac | B. | c(a-b)>0 | C. | ab2<cb2 | D. | ac(2a-2c)>0 |
10.过点(-1,2)且与直线y=$\frac{{\sqrt{3}}}{3}$x+2垂直的直线方程为( )
| A. | y-2=$\frac{\sqrt{3}}{3}$(x+1) | B. | y-2=$\sqrt{3}$(x+1) | C. | y-2=-$\frac{\sqrt{3}}{3}$(x+1) | D. | y-2=-$\sqrt{3}$(x+1) |
7.在等差数列{an}中,a2+a5=19,S5=40,则a1=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
 在三棱锥P-ABC中,面PAB、PAC、PBC两两垂直,且PA=2,PB=3,PC=4
在三棱锥P-ABC中,面PAB、PAC、PBC两两垂直,且PA=2,PB=3,PC=4