从一副未曾启封的扑克牌中取出1张红桃,2张黑桃的牌共3张,洗匀后,从这3张牌中任取1张牌恰好是黑桃的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,在△ABC中,已知∠C=90°,BC=5,AC=12,则它的内切圆周长是( )
如图,在△ABC中,已知∠C=90°,BC=5,AC=12,则它的内切圆周长是( )| A、5π | B、4π | C、2π | D、π |
下列函数中,y随x的增大而减小的是( )
| A、y=5x+1 | ||
| B、y=3x-2 | ||
C、y=-
| ||
| D、y=-1+9x |
对于如图①、②、③、④所示的四个平面图
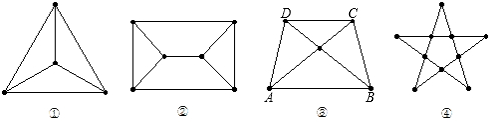
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
0 69554 69562 69568 69572 69578 69580 69584 69590 69592 69598 69604 69608 69610 69614 69620 69622 69628 69632 69634 69638 69640 69644 69646 69648 69649 69650 69652 69653 69654 69656 69658 69662 69664 69668 69670 69674 69680 69682 69688 69692 69694 69698 69704 69710 69712 69718 69722 69724 69730 69734 69740 69748 366461

我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
| 图 | 顶点数 | 边数 | 区域数 |
| ① | |||
| ② | |||
| ③ | 5 | 8 | 4 |
| ④ |
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
 两圆分别在Y,Z处的切线相交于X,设△O1O2B的外接圆为⊙O,直线XB交⊙O于另一点Q,若YO1与ZO2相交于点P.求证:
两圆分别在Y,Z处的切线相交于X,设△O1O2B的外接圆为⊙O,直线XB交⊙O于另一点Q,若YO1与ZO2相交于点P.求证: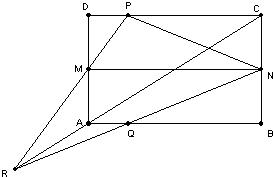 12、已知四边形ABCD是矩形,M、N分别是AD、BC的中点,P是CD上一点,Q是AB上一点,CP=BQ,PM与QN的交点为R.求证:R,A,C三点共线.
12、已知四边形ABCD是矩形,M、N分别是AD、BC的中点,P是CD上一点,Q是AB上一点,CP=BQ,PM与QN的交点为R.求证:R,A,C三点共线.