Question

已知⊙O₁与⊙O₂相交于点A，B，一条直线过A点分别与两圆相交于Y，Z，两圆分别在Y，Z处的切线相交于X，设△O₁O₂B的外接圆为⊙O，直线XB交⊙O于另一点Q，若YO₁与ZO₂相交于点P．求证：
（1）点P在⊙O上，且线段PQ是⊙O的一条直径；
（2）XQ=PQ．

Answer 1

分析：（1）连接BY，BZ，先证明点P在⊙O上，再证明Y，Z，B，P四点共圆，从而得到线段PQ是⊙O的一条直径；
（2）由△O₁EB∽△QEP，得

O1E

O1Y

=

O1E

O1B

=

QE

PQ

，又XY∥O₁Q得

O1E

O1Y

=

QE

XQ

，从而得出XQ=PQ．

解答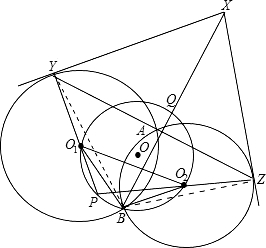：证明：（1）连接BY，BZ，
∠O₁PO₂=180°-∠O₁YA-∠O₂ZA=180°-∠O₁AY-∠O₂AZ=∠O₁AO₂=∠O₁BO₂
则∠YBZ=180°-（∠AYB+∠AZB）
=180°-（

1

2

∠AO₁B+

1

2

∠O₂AZ）
=180°-（∠BO₁O₂+∠BO₂O₁）
=∠O₁BO₂=∠O₁PO₂
=∠YPZ
所以Y，Z，B，P四点共圆，
又有∠XYP=∠XZP=90°知X，Y，P，Z四点共圆，所以B，X，Y，P，Z五点共圆，从而∠XBP=90°，即∠QBP=90°，
故线段PQ是⊙O的一条直径

（2）设XB，YP相交于点E，则

O1E

O1Y

=

O1E

O1B

=

QE

PQ

，（因为△O₁EB∽△QEP）
又由XY∥O₁Q（因为∠QO₁P=90°）得

O1E

O1Y

=

QE

XQ

，
所以PQ=XP

点评：本题考查了确定圆的条件、相似三角形的判定和性质，是一道综合题，难度较大．