题目内容
对于如图①、②、③、④所示的四个平面图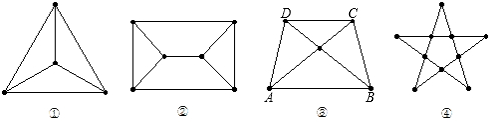
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
| 图 | 顶点数 | 边数 | 区域数 |
| ① | |||
| ② | |||
| ③ | 5 | 8 | 4 |
| ④ |
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
分析:(1)根据规定结合图形即可填充表格.
(2)根据所填的表格即可得出平面图的顶点数、边数、区域数之间的数量关系.
(3)根据(2)的关系列出方程,解出即可得出答案.
(2)根据所填的表格即可得出平面图的顶点数、边数、区域数之间的数量关系.
(3)根据(2)的关系列出方程,解出即可得出答案.
解答:解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,则边数有
x,所以x+9=
x+1,
解得:x=16.
这个平面图共有24条边.
| 图 | 顶点数 | 边数 | 区域数 |
| ① | 4 | 6 | 3 |
| ② | 6 | 9 | 4 |
| ③ | 5 | 8 | 4 |
| ④ | 10 | 15 | 6 |
(3)设顶点数为x,则边数有
| 3 |
| 2 |
| 3 |
| 2 |
解得:x=16.
这个平面图共有24条边.
点评:本题考查平面图形的知识,有一定难度,关键是理解题意,根据特殊推出一般规律.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
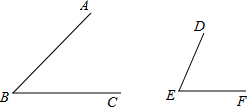 (2012•佛山)比较两个角的大小,有以下两种方法(规则)
(2012•佛山)比较两个角的大小,有以下两种方法(规则)