如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是（ ）
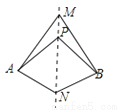
A. AM=BM B. AP=BN C. ∠MAP=∠MBP D. ∠ANM=∠BNM
D
【解析】试题解析：∵直线MN是四边形AMBN的对称轴，
∴点A与点B对应，
∴AM=BM，AN=BN，∠ANM=∠BNM，
∵点P时直线MN上的点，
∴∠MAP=∠MBP，
∴A，C，D正确，B错误，
故选B． 已知：如图，在Rt△ABC中，∠ACB=90°，∠A＜∠B，CM是斜边AB上的中线，将△ACM沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A的度数是（ ）
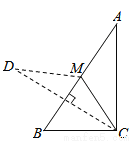
A．30° B．40° C．50° D．60°
A.
【解析】
试题解析：如图，
∵CM是斜边AB上的中线，
∴CM=AM=AB，
∴∠A=∠MCA（设为α）；
由翻折变换的性质得：∠DCM=∠MCA=α；
∵CD⊥AB，
∴∠DCA+∠A=90°，
即3α=90°，
∴∠A=α=30°．
故选A. 如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（ ）
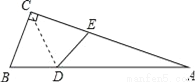
A. 44° B. 60° C. 67° D. 77°
C
【解析】试题分析：由∠ACB=90°，∠A=22°，三角形内角和是180º，可得∠B=90º-22º=68º，因为折叠角相等，所以∠CED=∠B=68º，∠BDC=∠EDC=∠BDE，，因为四边形内角和是360º，所以∠BDE=360º-90º-68º-68º=134º，所以∠BDC=∠BDE=×134º=67º．故选C． 如图，在矩形ABCD中，AB=10，BC=5点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A1、D1处，则阴影部分图形的周长为【 】
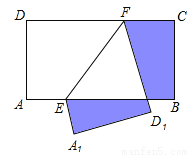
A.15 B.20 C.25 D.30
D
【解析】翻折变换（折叠问题），矩形和折叠的性质。
根据矩形和折叠的性质，得A1E=AE，A1D1=AD，D1F=DF，则阴影部分的周长即为矩形的周长，为2（10+5）=30。故选D。 如图,△ABC和△A'B'C'关于直线l对称.
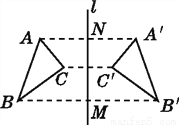
(1)△ABC____△A'B'C';
(2)A点的对应点是____,C'点的对应点是____;
(3)连接BB'交l于点M,连接AA'交l于点N,则BM=____,AA'与BB'的位置关系是____;
(4)直线l____AA'.
（1）≌ (2) A'点 C点 （3）B'M 互相平行 （4）垂直平分
【解析】根据轴对称的性质：关于某条直线对称的两个图形是全等图形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上.由此可得：(1)△ABC≌△A'B'C'; (2)A点的对应点是点A',C'点的对应点是点C; (3)连接BB'交l于... 如图,在由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有____个.
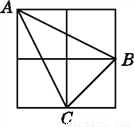
3
【解析】如图所示,符合条件的点共有3个. 请画出已知图形(如图所示)关于直线l的对称图形.(保留作图痕迹,不写画法)
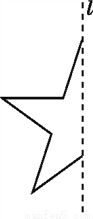
见解析
【解析】试题分析：观察题中图形，从图形中找到关键点向直线引垂线并延长相同长度，找到对应点，顺次连接即可．
试题解析：
如图: 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有多少个?画出图形.
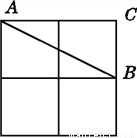
5个,图形见解析
【解析】试题分析：根据轴对称的定义画出图形即可，注意不要漏画图形.
试题解析：
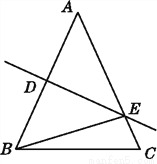
如图,与△ABC成轴对称且也以格点为顶点的三角形有5个. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
8
【解析】试题分析：由DE是△ABE的对称轴，根据轴对称的性质可得AE=BE，再由C△BCE=BC+CE+BE=14，可得BC+AC=14，从而求得AB的长.
试题解析：
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
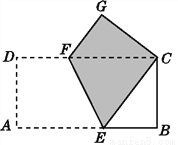
所以AB=AC=8. 如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
(1)见解析；（2）16
【解析】试题分析：（1）先证∠GCF=∠BCE，根据折叠性质，GC=AD=BC，∠G=∠D=∠B=90°根据ASA判定全等即可；（2）由（1）可知，阴影面积=四边形BCFE面积=矩形面积的一半，计算即可．
试题解析：
(1)因为∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.
又因为∠G=∠B=90°,GC=...