题目内容
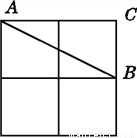
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有多少个?画出图形.
 5个,图形见解析
【解析】试题分析:根据轴对称的定义画出图形即可,注意不要漏画图形.
试题解析:
如图,与△ABC成轴对称且也以格点为顶点的三角形有5个.
5个,图形见解析
【解析】试题分析:根据轴对称的定义画出图形即可,注意不要漏画图形.
试题解析:
如图,与△ABC成轴对称且也以格点为顶点的三角形有5个.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列航空公司的标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
 C
【解析】A、B、D三个选项中的图形沿着一条直线折叠以后,直线两旁的部分均不能互相重合,只有C选项,沿着图中的一条直线(虚线)折叠,直线两旁的部分均能够互相重合,由此图形是轴对称图形,
故选择C.
C
【解析】A、B、D三个选项中的图形沿着一条直线折叠以后,直线两旁的部分均不能互相重合,只有C选项,沿着图中的一条直线(虚线)折叠,直线两旁的部分均能够互相重合,由此图形是轴对称图形,
故选择C. 下列代数式中,属于分式的是( )
A. -3 B. 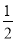 a-b
a-b
C. 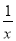 D. -4a3b
D. -4a3b
 C
【解析】根据整式和分式的定义,即可以对各选项进行判断.
【解析】
A. -3 是整式;
B. a-b是整式;
C. 是分式;
D. -4a3b是整式;
故选C.
C
【解析】根据整式和分式的定义,即可以对各选项进行判断.
【解析】
A. -3 是整式;
B. a-b是整式;
C. 是分式;
D. -4a3b是整式;
故选C. 化简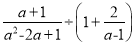 的结果是( )
的结果是( )
A. 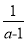 B.
B. 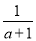
C. 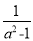 D.
D. 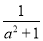
 A
【解析】试题解析:原式=
=
=
故选A.
A
【解析】试题解析:原式=
=
=
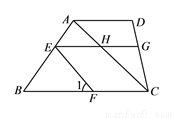
故选A. 如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
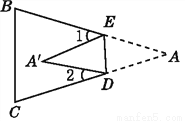
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)?
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
 (1)△EAD≌△EA'D,其中∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.(2)∠1=180°-2x,∠2=180°-2y;(3)∠1+∠2=2∠A
【解析】试题分析:(1)由轴对称的性质即可得结论;(2)结合(1)的结论,根据平角的定义可得结论;(3)表示出图中的△ABC、△ADE的内角和以及四边形BCDE的内角和,整理化简即可得到所求角之间的关系.
试题解析...
(1)△EAD≌△EA'D,其中∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.(2)∠1=180°-2x,∠2=180°-2y;(3)∠1+∠2=2∠A
【解析】试题分析:(1)由轴对称的性质即可得结论;(2)结合(1)的结论,根据平角的定义可得结论;(3)表示出图中的△ABC、△ADE的内角和以及四边形BCDE的内角和,整理化简即可得到所求角之间的关系.
试题解析... 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
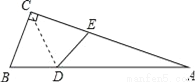
A. 44° B. 60° C. 67° D. 77°
 C
【解析】试题分析:由∠ACB=90°,∠A=22°,三角形内角和是180º,可得∠B=90º-22º=68º,因为折叠角相等,所以∠CED=∠B=68º,∠BDC=∠EDC=∠BDE,,因为四边形内角和是360º,所以∠BDE=360º-90º-68º-68º=134º,所以∠BDC=∠BDE=×134º=67º.故选C.
C
【解析】试题分析:由∠ACB=90°,∠A=22°,三角形内角和是180º,可得∠B=90º-22º=68º,因为折叠角相等,所以∠CED=∠B=68º,∠BDC=∠EDC=∠BDE,,因为四边形内角和是360º,所以∠BDE=360º-90º-68º-68º=134º,所以∠BDC=∠BDE=×134º=67º.故选C. 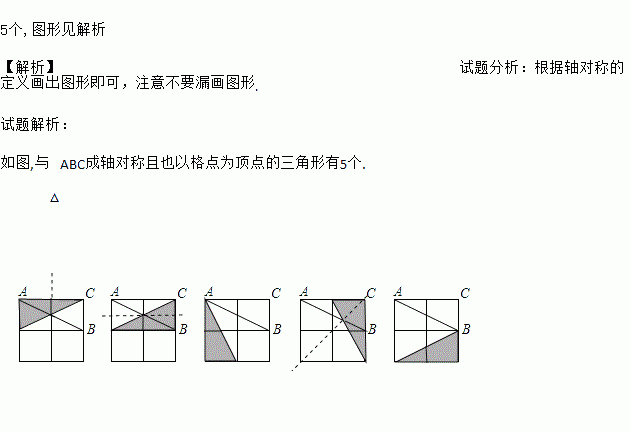

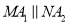 ,则
,则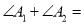 _________.
_________.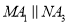 ,则
,则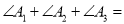 ___________.
___________.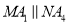 ,则
,则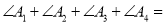 ___________.
___________.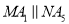 ,则
,则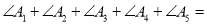 ___________.
___________.




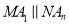 ,则
,则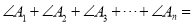 ______________.
______________. ,
,  和
和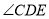 的平分线相交于
的平分线相交于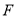 ,
, 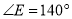 ,求
,求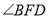 的度数.
的度数.
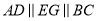 ,
, 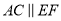 ,则图中与
,则图中与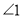 相等的角(不含
相等的角(不含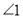 )有______个;若
)有______个;若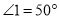 ,则
,则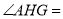 ________.
________.