无论a取何值时,下列分式一定有意义的是
A. 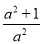 B.
B. 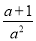 C.
C. 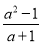 D.
D. 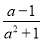
 D
【解析】试题解析:当a=0时,a2=0,故A、B中分式无意义;
当a=-1时,a+1=0,故C中分式无意义;
无论a取何值时,a2+1≠0,
故选D.
D
【解析】试题解析:当a=0时,a2=0,故A、B中分式无意义;
当a=-1时,a+1=0,故C中分式无意义;
无论a取何值时,a2+1≠0,
故选D. 当x=________时,分式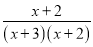 无意义.
无意义.
 -2或-3
【解析】根据分式无意义,则分母为0,列方程即可求解.
【解析】
∵分式无意义,
∴
解得,
故答案为:-2或-3.
-2或-3
【解析】根据分式无意义,则分母为0,列方程即可求解.
【解析】
∵分式无意义,
∴
解得,
故答案为:-2或-3. 已知x=1时,分式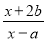 无意义,x=4时分式的值为0,求a+b的值.
无意义,x=4时分式的值为0,求a+b的值.
 -1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1.
-1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1. 当x=6时,分式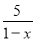 的值等于____.
的值等于____.
 -1
【解析】将x的值代入分式计算即可.
【解析】
当x=6时, ==-1.
故答案为:-1.
-1
【解析】将x的值代入分式计算即可.
【解析】
当x=6时, ==-1.
故答案为:-1. 当a=2016时,分式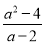 的值是_____.
的值是_____.
 2018
【解析】 = =a+2,
把a=2016代入得:
原式=2016+2=2018.
故答案为:2018.
2018
【解析】 = =a+2,
把a=2016代入得:
原式=2016+2=2018.
故答案为:2018. 在分式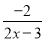 中,当x____时,分式有意义;当x____时,分式的值为正.
中,当x____时,分式有意义;当x____时,分式的值为正.
 ≠ <
【解析】(1)根据分母不为0则分式有意义,列不等式即可求解;
(2)利用有理数除法法则中的两数相除,同号得正,即分子、分母同负即可.
【解析】
(1)当,即x≠时,分式有意义;
(2)当,即x< 的值为正.
故答案为:≠;<.
≠ <
【解析】(1)根据分母不为0则分式有意义,列不等式即可求解;
(2)利用有理数除法法则中的两数相除,同号得正,即分子、分母同负即可.
【解析】
(1)当,即x≠时,分式有意义;
(2)当,即x< 的值为正.
故答案为:≠;<. 分式的概念:对于式子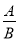 ,如果除式B中含有_____,那么称
,如果除式B中含有_____,那么称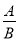 为分式,其中A称为分式的____,B称为分式的_____.
为分式,其中A称为分式的____,B称为分式的_____.
 字母 分子 分母
【解析】利用分式的概念即可得出答案.
【解析】
对于式子,如果除式B中含有字母,那么称为分式,其中A称为分式的分子,B称为分式的他、分母.
故答案为:字母;分子;分母.
字母 分子 分母
【解析】利用分式的概念即可得出答案.
【解析】
对于式子,如果除式B中含有字母,那么称为分式,其中A称为分式的分子,B称为分式的他、分母.
故答案为:字母;分子;分母. 分式有意义、无意义、值为0的条件:对于分式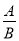 ,(1)当_____时,分式有意义;(2)当_____时,分式无意义;(3)当A=0且______时,分式的值为0.
,(1)当_____时,分式有意义;(2)当_____时,分式无意义;(3)当A=0且______时,分式的值为0.
 B≠0 B=0 B≠0
【解析】根据分母不等于0时分式有意义;分母等于0时分式无意义;分母不等于0且分子得0时,分式值为0即可得出答案.
【解析】
(1)当B≠0时,分式有意义;
(2)当B=0时,分式无意义;
(3)当A=0且B≠0时,分式的值为0.
故答案为:B≠0;B=0;B≠0.
B≠0 B=0 B≠0
【解析】根据分母不等于0时分式有意义;分母等于0时分式无意义;分母不等于0且分子得0时,分式值为0即可得出答案.
【解析】
(1)当B≠0时,分式有意义;
(2)当B=0时,分式无意义;
(3)当A=0且B≠0时,分式的值为0.
故答案为:B≠0;B=0;B≠0. 求使分式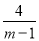 的值为整数的所有整数m的和.
的值为整数的所有整数m的和.
 6
【解析】利用整除的性质:即m-1是4的因数这一条件,即可求解.
【解析】
∵分式的值为整数,
∴m-1是4的因数,
又∵m为整数,
∴m=5,3,2,0,-1,-3,
则它们的和为5+3+2+0+(-1)+(-3)=6.
6
【解析】利用整除的性质:即m-1是4的因数这一条件,即可求解.
【解析】
∵分式的值为整数,
∴m-1是4的因数,
又∵m为整数,
∴m=5,3,2,0,-1,-3,
则它们的和为5+3+2+0+(-1)+(-3)=6. 下列式子是分式的是( )
A. 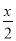 B.
B. 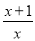 C.
C. 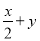 D.
D. 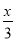
 B
【解析】根据分式的定义:一般地,如果A、B(B不等于零)表示两个整式,且B中含有字母,那么式子 就叫做分式.
【解析】
在式子, , , 中,分式有.
故选B.
B
【解析】根据分式的定义:一般地,如果A、B(B不等于零)表示两个整式,且B中含有字母,那么式子 就叫做分式.
【解析】
在式子, , , 中,分式有.
故选B.