正十边形的每个外角为________
36°
【解析】正十边形的一个外角为：360°÷10=36°，
故答案为：36°. 如图，在?ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（ ）
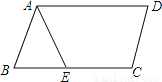
A．8cm B．6cm C．4cm D．2cm
C
【解析】
试题分析：【解析】
∵四边形ABCD是平行四边形，
∴BC=AD=12cm，AD∥BC，
∴∠DAE=∠BEA，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BEA=∠BAE，
∴BE=AB=8cm，
∴CE=BC﹣BE=4cm；
故答案为：C． □ABCD中，对角线AC与BD交于点O，∠DAC=42º，∠CBD=23º，则∠COD是（ ）．
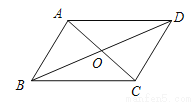
A. 61º B. 63º C. 65º D. 67º
C
【解析】试题分析：∵AD∥BC,∴∠BCA=∠DAC=42°，根据三角形的外角等于和它不相邻的内角和，∠COD=∠BCO+∠CBO=42°＋23°=65°，故选C． 如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（ ）
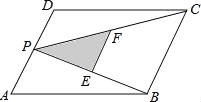
A．24 B．12 C．6 D．3
B
【解析】
试题分析：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，
∴四边形PQCD与四边形APQB都为平行四边形，
∴△PDC≌△CQP，△ABP≌△QPB，
∴S△PDC=S△CQP，S△ABP=S△QPB，
∵EF为△PCB的中位线，
∴EF∥BC，EF=BC，
∴△PEF∽△PBC，且相似比为1：2，
∴S△PEF：S... 如图，平行四边形ABCD的对角线AC、BD相交于点O，则下列说法一定正确的（ ）
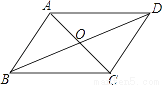
A. AO=OD B. AO⊥OD C. AO=OC D. AO⊥AB
C
【解析】试题分析：对角线不一定相等，A错误；
对角线不一定互相垂直，B错误；
对角线互相平分，C正确；
对角线与边不一定垂直，D错误．
故选C． 平行四边形ABCD的周长32，5AB=3BC，则对角线AC的取值范围为（ ）
A．6＜AC＜10 B.6＜AC＜16 C.10＜AC＜16 D.4＜AC＜16
D．
【解析】
试题分析：∵平行四边形ABCD的周长32，5AB=3BC，∴2（AB+BC）=2（BC+BC）=32，
∴BC=10，∴AB=6，∴BC﹣AB＜AC＜BC+AB，即4＜AC＜16．
故选D． 平行四边形的对角线一定具有的性质是（ ）
A. 相等 B. 互相平分
C. 互相垂直 D. 互相垂直且相等
B
【解析】试题分析：根据平行四边形的对角线互相平分可得答案．
【解析】
平行四边形的对角线互相平分，
故选：B． 如图，在?ABCD中，AB＝4，BC＝6，AC的垂直平分线交AD于点E，则△CDE的周长是( )
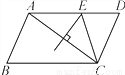
A. 7 B. 10 C. 11 D. 12
B
【解析】试题分析：根据线段垂直平分线的性质可得AE=EC，再根据平行四边形的性质可得DC=AB=4，AD=BC=6，进而可以算出△CDE的周长．
【解析】
∵AC的垂直平分线交AD于E，
∴AE=EC，
∵四边形ABCD是平行四边形，
∴DC=AB=4，AD=BC=6，
∴△CDE的周长为：EC+CD+ED=AD+CD=6+4=10，
故选：B．
... 如图，?ABCD中，BC=BD，∠C=74°，则∠ADB的度数是（ ）
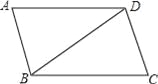
A. 16° B. 22° C. 32° D. 68°
C
【解析】试题分析：根据平行四边形的性质可知：AD∥BC，所以∠C+∠ADC=180°，再由BC=BD可得∠C=∠BDC=74°，进而可求出∠ADB=106°﹣74°=32°．
故选：C． 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（ ）
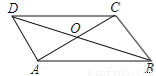
A．S□ABCD=4S△AOB
B．AC=BD
C．AC⊥BD
D．□ABCD是轴对称图形
A
【解析】
根据平行四边形的性质分别判断得出答案即可．