题目内容
□ABCD中，对角线AC与BD交于点O，∠DAC=42º，∠CBD=23º，则∠COD是（ ）．
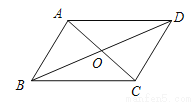
A. 61º B. 63º C. 65º D. 67º
C
【解析】试题分析：∵AD∥BC,∴∠BCA=∠DAC=42°，根据三角形的外角等于和它不相邻的内角和，∠COD=∠BCO+∠CBO=42°＋23°=65°，故选C．
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案分式方程
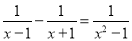去分母时，两边都乘以________.
(x+1)(x-1))
【解析】∵分式方程 可化为： ，
∴去分母时，方程两边应都乘以： . 如图，杭州市郊外一景区内有一条笔直的公路a经过两个景点A，B，景区管委会又开发了风景优美的景点C，经测量景点C位于景点A的北偏东60°方向，又位于景点B的北偏东30°方向，且景点A、B相距200m，则景点B、C相距的路程为（ ）
A. 100
B. 200 C. 100 D. 200
B
【解析】试题分析：根据方位角可得：∠A=30°，∠CBA=120°，则∠C=30°，则△ABC为等腰三角形，故BC=AB=200m，故选B． 平行四边形的一条边长是12cm，那么它的两条对角线的长可能是（ ）
A. 8cm和16cm B. 10cm和16cm C. 8cm和14cm D. 8cm和12cm
B
【解析】试题解析：对于A，两条对角线的一半长分别为4cm，8cm，由于4+8=12，故不能构成三角形，故A不符合题意；
对于B，两条对角线的一半长分别为5cm，8cm，由于5+8＞12，故能构成三角形，故B符合题意；
对于C，两条对角线的一半长分别为4cm，7cm，由于4+7＜12，故不能构成三角形，故C不符合题意；
对于D，两条对角线的一半长分别为4cm，6cm，由于... 如图，在?ABCD中，AB＝4，BC＝6，AC的垂直平分线交AD于点E，则△CDE的周长是( )
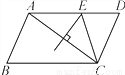
A. 7 B. 10 C. 11 D. 12
B
【解析】试题分析：根据线段垂直平分线的性质可得AE=EC，再根据平行四边形的性质可得DC=AB=4，AD=BC=6，进而可以算出△CDE的周长．
【解析】
∵AC的垂直平分线交AD于E，
∴AE=EC，
∵四边形ABCD是平行四边形，
∴DC=AB=4，AD=BC=6，
∴△CDE的周长为：EC+CD+ED=AD+CD=6+4=10，
故选：B．
... 一个四边形剪去一三角形后余下的多边形为 ___________ 边形
三、四、五
【解析】如图可知，一个四边形截去一个三角形后变成三角形或四边形或五边形，
故答案为：三、四、五. 四边形ABCD中，若∠A+∠C+∠D=280°，则∠B的度数为( )
A. 80° B. 90° C. 170° D. 20°
A
【解析】试题分析：四边形的内角和为360°，
∴∠B＝360°－(∠A＋∠C＋∠D)
＝360°－280°
＝80°，
故选A． 为改善环境，张村拟在荒山上种植960棵树，由于共青团员的支持，每日比原计划多种20棵，结果提前4天完成任务，原计划每天种植多少棵？设原计划每天种植x棵，根据题意得方程______________.
【解析】设原计划每天种植x棵，根据题意：
故答案： . 计算：（1）
＝________；（2）
=______________．
【解析】试题解析：(1)原式
(2)原式
故答案为：(1) (2) .