如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）探究下列问题：
①若一个函数的特征数为[2，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[4，2]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[2，4]？
（1）此函数图象的顶点坐标为：（1，0）；（2）图象对应的函数的特征数为：[0，﹣1]；（3）原函数的图象向右平移1个单位，再向上平移5个单位得到．
【解析】试题分析：（1）根据特征数的定义，得二次函数为y=x2﹣2x+1，再利用配方得：y=（x﹣1）2，从而顶点坐标为（1,0）
（2）①根据特征数的定义，得二次函数为y=x2+2x-1，再利用配方得y=（x+1）2﹣2，图象先向右平移... 把代数式xy2﹣9x分解因式，结果正确的是（ ）
A. x（y2﹣9） B. x（y+3）2 C. x（y+3）（y﹣3） D. x（y+9）（y﹣9）
C
【解析】xy2﹣9x=x(y2-9)=x(y+3)(y-3),故选C. 下列各式从左到右的变形中，是分解因式的是 ( )
A. x2-9+6x＝(x+3)(x-3)+6x B. (x+5)(x-2)＝x2+3x-10
C. x2-8x+16＝(x-4)2 D. (x-2)(x+3)＝(x+3)(x-2)
C
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得，只有选项C符合因式分解的形式，故选C. 观察下面算962×95+962×5的解题过程，其中最简单的方法是( )
A. 962×95+962×5＝962×(95+5)＝962×100＝96200
B. 962×95+962×5＝962×5×(19+1)＝962×(5×20) ＝96200
C. 962×95+962×5＝5×(962×19+962)＝5×(18278+962)＝96200
D. 962×95+962×5＝91390+4810＝96200
A
【解析】计算962×95+962×5的值，最简单的方法先提取公因式962，即962×95+962×5＝962×(95+5)＝962×100＝96200，故选A. 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
故选：C. 下列各式从左到右的变形（1）15x2y=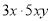
；（2）(x+y)(x-y)=x2-y2；
（3）x2-6x+9=(x-3)2；（4）x2+4x+1=x(x+4+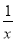
)，其中是因式分解的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得只有（3）符合要求，故选A. 下列各式的因式分解中正确的是（ ）
A. -m2+mn-m=-m(m+n-1) B. 9abc-6a2b2=3abc(3-2ab)
C. 3a2x-6bx+3x=3x(a2-2b) D.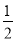 
ab2+
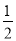a2b=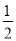
ab(a+b)
D
【解析】选项A，原式=-m(m-n+1)；选项B，原式=3abc(3c-2ab)；选项C，原式=3x(a2-2b+1)；选项D，原式=ab(a+b)；故选D. 把多项式(m+1)（m-1）+（m-1）分解因式，一个因式是（m-1）,则另一个因式是（ ）
A. m+1 B. 2m C. 2 D. m+2
D
【解析】∵(m+1)（m-1）+（m-1）=（m-1）（m+1+1）=（m-1）（m+2），
∴另一个因式是（m+2）.
故选D. 已知不论x为何值，x2-kx-15=(x+5)(x-3)，则k值为（ ）
A. 2 B. -2 C. 5 D. -3
B
【解析】∵x2-kx-15=(x+5)(x-3)=x2+2x-15，
∴k=-2.
故选B. (-2)2001+(-2)2002等于（ ）
A. -22001 B. -22002 C. 22001 D. -2
C
【解析】(-2)2001+(-2)2002=(-2)2001×(1-2)=22001，故选C.