下列能断定△ABC为等腰三角形的是（ ）
A.∠A=30°，∠B=60° B.∠A=50°，∠B=80°
C.AB=AC=2，BC=4 D.AB=3，BC=7，周长为10
B
【解析】
试题分析：A、B根据三角形的内角和求出第三个角，可得结果；C不能组成三角形，D利用周长求出第三边即可得到答案，根据等腰三角形的判定，采用逐条分析排除的方法判断．
【解析】
A、根据三角形内角和定理得，∠C=180°﹣60°﹣30°=90°，故不是等腰三角形；
B、根据三角形内角和定理得，∠C=180°﹣50°﹣80°=50°，故是等腰三角形；
C、根据... 如图所示，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于( )
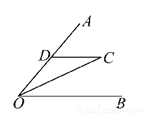
A. 3cm B. 4cm C. 1.5cm D. 2cm
A
【解析】试题分析：根据角平分线的性质可得：∠DOC=∠COB，根据平行线的性质可得：∠DCO=∠COB，则∠DOC=∠DCO，则CD=OD=3cm，故选A． 如图，在△ABC中，∠B≠∠C，求证：AB≠AC.当用反证法证明时，第一步应假设( )
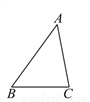
A. ∠B＝∠C B. AB＝AC C. AB＝BC D. ∠A＝∠B
B
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即AB=AC，故选B． 在△ABC中，∠B＝40°，∠C＝70°，则△ABC中是 三角形
等腰
【解析】本题考查的是三角形的分类。∠C=180°-40°-70°＝70°，所以∠A＝∠C=70°故为等腰三角形。 如图，四边形ABCD沿直线l对折后互相重合，如果AD∥BC，那么△ABC___(填“是”或“不是”)等腰三角形．
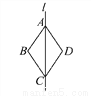
是
【解析】试题分析：根据折叠图形的性质可知：∠BAC=∠DAC，根据平行线的性质可知：∠DAC=∠ACB，则∠BAC=∠ACB，即△ABC为等腰三角形． 用反证法证明命题“对顶角相等”第一步假设__________________.
对顶角不相等
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，即先假设“对顶角不相等”． 如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：_____.
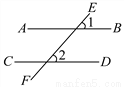
AB∥CD
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即应先假设AB∥CD． 已知△ABC中，AB＝AC，求证∠B＜90°，下面写出了用反证法证明过程中的四个步骤：①所以∠B＋∠C＋∠A＞180°，这与三角形内角和定理相矛盾；②所以∠B＜90°；③假设∠B≥90°；④那么由AB＝AC，得∠B＝∠C≥90°，即∠B＋∠C≥180°.这四个步骤正确的顺序应是_________(填序号)．
③④①②
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，然后根据已知条件得出与定理相矛盾，最后得出假设不成立，得出答案，故正确的序号是：③④①②． 如图，在△ABC中，AB＝AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F.
求证：△AEF是等腰三角形．
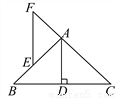
见解析
【解析】试题分析：首先根据等腰三角形底边上的三线合一定理可得：AD为∠BAC的角平分线，根据平行线的性质得出∠F=∠CAD，∠FEA=∠BAD，从而∠FEA=∠F，得出等腰三角形．
试题解析：∵AB=AC，AD⊥BC， ∴∠BAD=∠CAD， 又∵AD∥EF，
∴∠F=∠CAD，∠FEA=∠BAD， ∴∠FEA=∠F， ∴△AEF是等腰三角形．