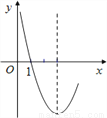
如图，二次函数y=x2-6x+n的部分图象如图所示，若关于x的一元二次方程x2-6x+n=0的一个解为x1=1，则另一个解x2= ___________.
5．
【解析】试题分析：根据二次函数的图象与x轴的交点关于对称轴对称，直接求出x2的值．
试题解析：由图象知，对称轴为x=-
根据二次函数的图象的对称性，
解得：x2=5． 抛物线y=2x2+4x+m与x轴只有一个公共点，则m的值为____
2
【解析】∵抛物线与x轴只有一个公共点，
∴△=0，
∴b2-4ac=42-4×2×m=0；
∴m=2．
故答案为：2. 如图，抛物线y= -x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y____0（填“＞”“=”或“＜”号）．
＜
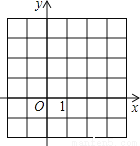
【解析】试题分析：根据题意可得函数的对称轴为x=1，∵0＜＜1，则1＜＜2，∴x=－2＜0，根据图象可得：当x＜0时，y＜0. （1）请在坐标系中画出二次函数y=x2﹣2x的大致图象；
（2）根据方程的根与函数图象的关系，将方程x2﹣2x=1的根在图上近似的表示出来（描点）；
（3）观察图象，直接写出方程x2﹣2x=1的根．（精确到0.1）
【解析】
（1）如下图，
y=x2﹣2x=（x﹣1） 2﹣1，
作出顶点，作出与x轴的交点，图象光滑．
（2）正确作出点M，N；
（3）写出方程的根为﹣0.4，2.4．
【解析】
（1）确定顶点坐标和与x轴y轴交点，作出图形；
（2）方程x2﹣2x=1的根就是二次函数y=x2﹣2x的函数值为1时的横坐标x的值；
（3）观察图象可知图象交点的横坐标即... 已知一元二次方程x2+px+q+1=0的一根为2．
（1）求q关于p的关系式；
（2）求证：抛物线y=x2+px+q与x轴有两个交点；
（1）q= -2p-5；（2）见解析
【解析】试题分析：（1）把x=2代入可求得q与p的关系式；
（2）由△=b2-4ac可判断抛物线与x轴的交点情况.
试题解析：（1）把x=2代入得22+2p+q+1=0，即q= -2p-5；
（2）∵△=p2-4q＞0，
由（1）得△=p2+4（2p+5）=p2+8p+20=（p+4）2+4＞0，
∴一元二次方程x2+px+... 已知二次函数y=x2+2x+c的图象经过点（1，-5）．
（1）求c的值；
（2）求函数图象与x轴的交点坐标．
（1）8；（2）（-4，0），（2，0）
【解析】试题分析：（1）二次函数解析式只有一个待定系数c，把点（1，-5）代入解析式即可求c；
（2）已知二次函数解析式求函数图象与x轴的交点坐标，令y=0，解一元二次方程，可得交点的横坐标．
试题分析：（1）∵点（1，-5）在y=x2+2x+c的图象上，
∴-5=1+2+c，
∴c= -8；
（2）令y=0，则x2+2... 已知y关于x的函数：y=（k-2）x2-2（k-1）x+k+1中满足k≤3．
求证：此函数图象与x轴总有交点；
见解析
【解析】试题分析：本题可将函数分成一次函数和二次函数两种情况讨论：当k=2时，函数为一次函数，与x轴一定有交点；当k≠2时，函数为二次函数，让y=0，根据根与系数的关系以及k的取值范围我们可判断出此时的方程是否有解，如果有解，则必与x轴有交点．
试题解析：分两种情况：
（1）当k=2时，函数为y= -2x+3，图象与x轴有交点．
（2）当k≠2时，△=4（k-1）2... 已知抛物线y= -x2+mx+（7-2m）（m为常数）．
（1）证明：不论m为何值，抛物线与x轴恒有两个不同的交点；
（2）若抛物线与x轴的交点A（x1，0）、B（x2，0）的距离为AB=4（A在B的左边），且抛物线交y轴的正半轴于C，求抛物线的解析式．
（1）证明见解析；（2）抛物线的解析式为y= -x2+2x+3．
【解析】试题分析：（1）要证明抛物线与x轴恒有两个不同的交点证明抛物线的判别式是正数，所以证明判别式是正数即可解决问题；
（2）首先由AB=4可以得|x2-x1|=4，而（x2-x1）2=（x2-x1）2-4x1x2=16，然后利用根与系数的关系即可得到关于m方程，解方程即可求出m，也就求出了抛物线的解析式．
试题... 在直角坐标系中，将点P(－3,2)向沿y轴方向向上平移4个单位长度后，得到的点坐标为( )
A. (－3,6) B. (1,2) C. (－7,2) D. (－3，－2)
A
【解析】因为点沿y轴向上移动,横坐标不变,纵坐标加上平移单位,将点P(－3,2)向沿y轴方向向上平移4个单位长度后,得到的点坐标为(－3,6),故选A. 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
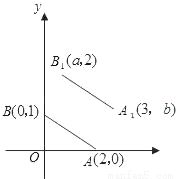
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A.