在□ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
D．
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，AB∥CD，
∴∠B+∠C=180°，∠A+∠D=180°，
即∠A和∠C的数相等，∠B和∠D的数相等，且∠B+∠C=∠A+∠D，
故选D． 平行四边行的两条对角线把它分成全等三角形的对数是（ ）
A. 2 B. 4 C. 6 D. 8
B
【解析】【解析】
如图，?ABCD中，AC，DB分别分得△ABC≌△CDA，△ABD≌△CDB，
又对角线互相平分得到△AOD≌△COB，△AOB≌△COD，所以有4对．
故选B． 在□ABCD中，∠A、∠B的度数之比为5∶4，则∠C等于（ ）
A. 60° B. 80° C. 100° D. 120°
C
【解析】试题分析：解题的关键是熟练掌握平行四边形的邻角互补、对角相等．根据平行四边形的性质可得∠A、∠B互补，从而可求得∠A的度数，即可得到结果．
∵□ABCD，
∴∠A+∠B =180°，
∵∠A、∠B的度数之比为5∶4，
∴∠C =∠A=100°．
故选C． □ABCD的周长为36 cm，AB=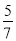
BC，则较长边的长为（ ）
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
D
【解析】【解析】
∵?ABCD的周长=2（AB+BC）=36，∴AB+BC=18．∵AB=BC，∴BC=10.5．
故选D． 如图，平行四边形ABCD中，EF过对角线的交点O，AB＝4，AD＝3，OF＝1.3，则四边形BCEF的周长为（ ）
A. 8.3 B. 9.6 C. 12.6 D. 13.6
B
【解析】【解析】
根据平行四边形的中心对称性得：OF=OE=1.3．∵?ABCD的周长=（4+3）×2=14
∴四边形BCEF的周长=×?ABCD的周长+2.6=9.6．故选B． 在□ABCD中，对角线AC，BD相交于O点，AC＝10，BD＝8，则AD长的取值范围是 （ ）
A. AD＞1 B. AD＜9 C. 1＜AD＜9 D. AD＞10
C
【解析】【解析】
平行四边形的对角线互相平分得：两条对角线的一半分别是5，4．再根据三角形的三边关系，得：1＜AD＜9．故选C． 下列不能作为判定四边形ABCD为平行四边形的条件的是（ ）
A. AB＝CD，AD＝BC B. AB
CD
C. AB＝CD，AD∥BC D. AB∥CD，AD∥BC
C
【解析】解：A．∵AB=CD，AD=BC，∴四边形ABCD的两组对边相等，可以判定四边形ABCD是平行四边形；故本选项不合题意；
B．∵AB∥CD，AB=CD，∴四边形ABCD的一组对边平行且相等，可以判定四边形ABCD是平行四边形；故本选项不合题意；
C．∵AB=CD，AD∥CD，无法判定四边形ABCD是平行四边形；故本选项合题意；
D．∵AB∥CD，AD∥BC，四边... 如图所示，梯形ABCD中AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A′处，若∠A′BC＝20°，则∠A′BD的度数为（ ）
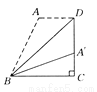
A. 15° B. 20° C. 25° D. 30°
C
【解析】∵∠A′BC=20°
∴∠BA′C=70°
∴∠DA′B=110°
∴∠DAB=110°
∴∠ABC=70°
∴∠ABA′=∠ABC﹣∠A′BC=70°﹣20°=50°
∴∠A′BD=∠ABA′=25°．
故选C． 在等腰梯形ABCD中，AD∥BC，AE⊥BC于E，且AE=AD，BC＝3AE， 则∠BAD等于 （ ）
A. 120° B. 135° C. 130° D. 不能确定
B
【解析】【解析】
过点D作DF⊥BC于点F．
∵AE⊥BC，DF⊥BC，AD=AE，∴四边形AEFD为正方形，∴AD=EF．
∵AD=AE，BC=3AD，∴BE=AE=EF=FC，∴∠B=45°，∴∠BAD=135°．
故选B． 已知□ABCD中，∠B=70°，则∠A=______，∠C=______，∠D=______.
110° 110° 70°
【解析】【解析】
由平行四边形的性质得：∠A=180°-∠B=110°，∠C=∠A=70°，∠D=180°-∠B=110°．
故答案为：110°，110°，70°．