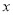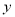从地面竖直向上抛出一个小球，小球的高度h（米）与运动时间t（秒）之间的关系式为h=30t﹣5t2，那么小球抛出 秒后达到最高点．
3
【解析】试题分析：首先理解题意，先把实际问题转化成数学问题后，知道解此题就是求出h=30t﹣5t2的顶点坐标即可．
【解析】
h=﹣5t2+30t，
=﹣5（t2﹣6t+9）+45，
=﹣5（t﹣3）2+45，
∵a=﹣5＜0，
∴图象的开口向下，有最大值，
当t=3时，h最大值=45；
即小球抛出3秒后达到最高点．
故答案为：3．
... 二次函数
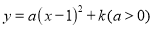中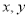
的几组对应值如下表．
| -2 | 1 | 5 |
| m | n | p |
表中m、n、p的大小关系为________________（用“＜”连接）
n＜m＜p
【解析】【解析】
设（-2，m）关于对称轴的对称点为（x，m）．∵二次函数的对称轴为x=1，∴ ，解得：x=4．∵a＞0，∴抛物线开口向上，在对称轴右侧，y随x的增大而增大．∵1＜4＜5，∴n＜m＜p．故答案为：n＜m＜p． 在第一象限内作射线OC，与x轴的夹角为60°，在射线OC上取一点A，过点A作AH⊥x 轴于点H，在抛物线y=x2（x＞0）上取一点P，在y轴上取一点Q，使得以P、O、Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是______．
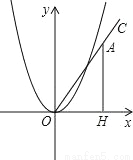
【解析】试题解析：①如图1，当∠POQ=∠OAH=30°，若以P，O，Q为顶点的三角形与△AOH全等，那么A、P重合；
∵∠AOH=60°，
∴直线OA：y=x，
联立抛物线的解析式得： ，
解得： 或，
故A（，3）；
②当∠POQ=∠AOH=60°，此时△POQ≌△AOH，
易知∠POH=30°，则直线y=x，联立抛物线的解析式，得： ，
解得：... 已知抛物线y=ax2+bx+3的对称轴是直线x=1．
（1）求证：2a+b=0；
（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．
（1）见解析；（2）x=－2
【解析】试题分析：直接利用对称轴公式代入求出即可；根据（1）中所求，再将x=4代入方程求出a，b的值，进而解方程得出即可．
试题解析：（1）证明：∵对称轴是直线x=1=﹣，∴b=－2a ∴2a+b=0；
（2）∵ax2+bx﹣8=0的一个根为4，∴16a+4b﹣8=0，∵b=﹣2a，∴16a﹣8a﹣8=0，
解得：a=1，则b=﹣2，∴a+bx... 如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
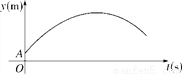
（1）足球飞行的时间是s时，足球离地面最高，最大高度是4.5m；（2）能.
【解析】试题分析：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），于是得到，求得抛物线的解析式为：y=﹣t2+5t+，当t=时，y最大=4.5；
（2）把x=28代入x=10t得t=2.8，当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，于是得到他能将球直... 已知二次函数的图象经过点（0，﹣3），且顶点坐标为（﹣1，﹣4）．
（1）求该二次函数的解析式；
（2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积．
1.【解析】
（1）设，把点代入得：-----------2分
∴函数解析式或-----------------------------2分
2.（2）∵，解得，
∴，，。---------（2分）
∴△ABC的面积=。--------------------------（2分）
【解析】试题分析：（1）先设所求函数解析式是y=a（x+1）2﹣4，再把（0，﹣3）代... 如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元．
探究1：如果木板边长为1米，FC=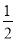
米，则一块木板用墙纸的费用需 元；
探究2：如果木板边长为2米，正方形EFCG的边长为x米，一块木板需用墙纸的费用为y元，
（1）用含x的代数式表示y（写过程）．
（2）如果一块木板需用墙纸的费用为225元，求正方形EFCG的边长为多少米？
（1）55，y=20x2﹣40x+240（2）正方形EFCG的边长为或米
【解析】【解析】
探究1：∵四边形ABCD是正方形，
∴AB=BC=CD=DA=1，
∴S正方形ABCD=1，
∵四边形EFCG是正方形，
∴EF=CF=，
∴S正方形EFCG=，BF=，
∴S△ABE==
∴空白部分的面积为：1﹣﹣=，
∴这块木板用墙纸的费用为：+8... 已知二次函数y=2x2+bx﹣1．
（1）求证：无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）若两点P（﹣3，m）和Q（1，m）在该函数图象上．
①求b、m的值；
②将二次函数图象向上平移多少单位长度后，得到的函数图象与x轴只有一个公共点？
（1）无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）b=4，m=5；（3）二次函数图象向上平移3个单位
【解析】
试题分析：（1）先计算判别式的值，再利用非负数的性质可判断△=＞0，然后根据判别式的意义可判断抛物线与x轴必有两个交点；
（2）①先利用抛物线的对称性可确定抛物线的对称轴方程，从而可求出b的值，然后计算自变量为1所对应的函数值即可得... 已知二次函数y=2x2+bx﹣1．
（1）求证：无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）若两点P（﹣3，m）和Q（1，m）在该函数图象上．
①求b、m的值；
②将二次函数图象向上平移多少单位长度后，得到的函数图象与x轴只有一个公共点？
（1）无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）b=4，m=5；（3）二次函数图象向上平移3个单位
【解析】
试题分析：（1）先计算判别式的值，再利用非负数的性质可判断△=＞0，然后根据判别式的意义可判断抛物线与x轴必有两个交点；
（2）①先利用抛物线的对称性可确定抛物线的对称轴方程，从而可求出b的值，然后计算自变量为1所对应的函数值即可得... 若将抛物线y=2x2向上平移3个单位，所得抛物线的解析式为（ ）
A．y=2x2+3 B．y=2x2﹣3 C．y=2（x﹣3）2 D．y=2（x+3）2
A．
【解析】
试题分析：由“上加下减”的原则可知，将二次函数y=2x2向上平移3个单位可得到函数y=2x2+3，
故选：A．