题目内容
从地面竖直向上抛出一个小球,小球的高度h(米)与运动时间t(秒)之间的关系式为h=30t﹣5t2,那么小球抛出 秒后达到最高点.
 3
【解析】试题分析:首先理解题意,先把实际问题转化成数学问题后,知道解此题就是求出h=30t﹣5t2的顶点坐标即可.
【解析】
h=﹣5t2+30t,
=﹣5(t2﹣6t+9)+45,
=﹣5(t﹣3)2+45,
∵a=﹣5<0,
∴图象的开口向下,有最大值,
当t=3时,h最大值=45;
即小球抛出3秒后达到最高点.
故答案为:3.
...
3
【解析】试题分析:首先理解题意,先把实际问题转化成数学问题后,知道解此题就是求出h=30t﹣5t2的顶点坐标即可.
【解析】
h=﹣5t2+30t,
=﹣5(t2﹣6t+9)+45,
=﹣5(t﹣3)2+45,
∵a=﹣5<0,
∴图象的开口向下,有最大值,
当t=3时,h最大值=45;
即小球抛出3秒后达到最高点.
故答案为:3.
...
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
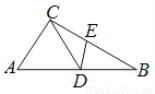
A. 50° B. 51° C. 51.5° D. 52.5°
 D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D.
D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D. 如图,抛物线y=﹣x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).
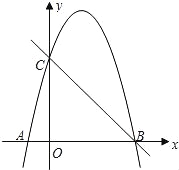
(1)OB=_________,抛物线的顶点坐标为_________________;
(2)当n=4时,求点P关于直线BC的对称点P′的坐标;
(3)是否存在直线PD,使直线PD所对应的一次函数随x的增大而增大?若存在,直接写出m的取值范围;若不存在,请说明理由.
 (1)4,(,);(2)(0,1);(3)1<m<2.
【解析】
试题分析:(1)当y=0时,即﹣x2+3x+4=0,解得:x1=4,x2=﹣1,∴点A(﹣1,0)点B(4,0),∴OB=4,y=﹣x2+3x+4=,∴抛物线的顶点坐标为(,),故答案为:4,(,).
(2)如图,连接CP,CP′,
n=4时,﹣m2+3m+4=4,解得:m1=3,m2=0(舍去),∴这时P点...
(1)4,(,);(2)(0,1);(3)1<m<2.
【解析】
试题分析:(1)当y=0时,即﹣x2+3x+4=0,解得:x1=4,x2=﹣1,∴点A(﹣1,0)点B(4,0),∴OB=4,y=﹣x2+3x+4=,∴抛物线的顶点坐标为(,),故答案为:4,(,).
(2)如图,连接CP,CP′,
n=4时,﹣m2+3m+4=4,解得:m1=3,m2=0(舍去),∴这时P点... 在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 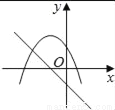 B.
B. 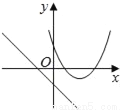 C.
C. 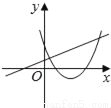 D.
D. 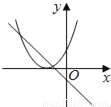
 D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<...
D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<... 已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
 1.【解析】
(1)设,把点代入得:-----------2分
∴函数解析式或-----------------------------2分
2.(2)∵,解得,
∴,,。---------(2分)
∴△ABC的面积=。--------------------------(2分)
【解析】试题分析:(1)先设所求函数解析式是y=a(x+1)2﹣4,再把(0,﹣3)代...
1.【解析】
(1)设,把点代入得:-----------2分
∴函数解析式或-----------------------------2分
2.(2)∵,解得,
∴,,。---------(2分)
∴△ABC的面积=。--------------------------(2分)
【解析】试题分析:(1)先设所求函数解析式是y=a(x+1)2﹣4,再把(0,﹣3)代... 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正确的结论的个数是( )
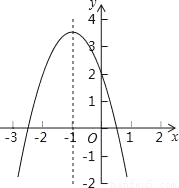
A. 1 B. 2 C. 3 D. 4
 C
【解析】①∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x==﹣1,∴b=2a<0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,所以①正确;
②∵抛物线与x轴有2个交点,∴△=b2-4ac>0,∴4ac
C
【解析】①∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x==﹣1,∴b=2a<0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,所以①正确;
②∵抛物线与x轴有2个交点,∴△=b2-4ac>0,∴4ac 关于二次函数y=x2﹣2x﹣3的图象,下列说法中错误的是( )
A. 当x<2,y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是(0,﹣3)
 A
【解析】试题分析:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线开口向上,对称轴为x=1,当x<1时y随x的增大而减小,故B、C正确,A不正确,
令x=0可得y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故D正确,
故选A.
A
【解析】试题分析:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线开口向上,对称轴为x=1,当x<1时y随x的增大而减小,故B、C正确,A不正确,
令x=0可得y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故D正确,
故选A. 如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

 答案见解析
【解析】试题分析:要证明四边形ACEF是平行四边形,需求证CE∥AF,由已知易得△BEC,△AEF是等腰三角形,则∠1=∠2,∠3=∠F,又∠2=∠3,得到∠1=∠F,故CE∥AF,由此即可得到结论.
试题解析:证明:∵点E为AB中点,∴AE=EB.又∵∠ACB=90°,∴CE=AE=EB.又∵AF=CE,∴AF=AE,∴∠3=∠F.又∵EB=EC,ED⊥BC,∴∠1=∠2...
答案见解析
【解析】试题分析:要证明四边形ACEF是平行四边形,需求证CE∥AF,由已知易得△BEC,△AEF是等腰三角形,则∠1=∠2,∠3=∠F,又∠2=∠3,得到∠1=∠F,故CE∥AF,由此即可得到结论.
试题解析:证明:∵点E为AB中点,∴AE=EB.又∵∠ACB=90°,∴CE=AE=EB.又∵AF=CE,∴AF=AE,∴∠3=∠F.又∵EB=EC,ED⊥BC,∴∠1=∠2... 以长为5cm, 4cm, 7cm的三条线段中的的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是 ( )
A. 1 B. 2 C. 3 D. 4
 C
【解析】【解析】
分别以4cm,5cm为边,7cm为对角线;或以4cm,7cm为边,5cm为对角线;或5cm,7cm为边,4cm为对角线共有三种情况.故选C.
C
【解析】【解析】
分别以4cm,5cm为边,7cm为对角线;或以4cm,7cm为边,5cm为对角线;或5cm,7cm为边,4cm为对角线共有三种情况.故选C. 
