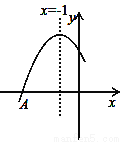
如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出以下结论：①abc＜0 ②b2﹣4ac＞0 ③4b+c＜0 ④若B（﹣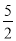
，y1）、C（﹣
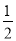，y2）为函数图象上的两点，则y1＞y2⑤当﹣3≤x≤1时，y≥0，
其中正确的结论是（填写代表正确结论的序号）__________________．
②③⑤
【解析】【解析】
由图象可知，a＜0，b＜0，c＞0，∴abc＞0，故①错误．
∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故②正确．
∵抛物线对称轴为x=﹣1，与x轴交于A（﹣3，0），∴抛物线与x轴的另一个交点为（1，0），∴a+b+c=0，﹣ =﹣1，∴b=2a，c=﹣3a，∴4b+c=8a﹣3a=5a＜0，故③正确．
∵B（﹣，y1）、C（﹣，y2）为函... 将抛物线y=x2﹣4x+4沿y轴向下平移9个单位，所得新抛物线与x轴正半轴交于点B，与y轴交于点C，顶点为D．求：（1）点B、C、D坐标；（2）△BCD的面积．
（1）（5，0）；（2）15.
【解析】试题分析：
（1）先由图象平移的规律求出抛物线的解析式，配方后可得顶点D的坐标，设y=0，可得B的坐标，设x=0，可得C的坐标；
（2）过D作DA⊥y轴于点A，根据图形的面积的和与差求△BCD的面积.
试题解析：
（1）抛物线y=x2﹣4x+4沿y轴向下平移9个单位后解析式是y=x2﹣4x+4﹣9，即y=x2﹣4x﹣5．
... 在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．
（1）记抛物线顶点为D，求△BCD的面积；
（2）若直线y=﹣
x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．
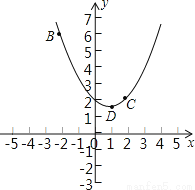
（1）3 （2）＜b≤3．
【解析】（1）根据待定系数法即可解决问题．求出直线BC与对称轴的交点H，根据S△BDC=S△BDH+S△DHC即可解决问题．
（2）由，当方程组只有一组解时求出b的值，当直线y=﹣x+b经过点C时，求出b的值，当直线y=﹣x+b经过点B时，求出b的值，由此即可解决问题．
【解析】
（1）由题意解得，
∴抛物线解析式为y=x2﹣x+2．
∵... 平面直角坐标系xOy中，对称轴平行于y轴的抛物线过点A（1，0）、B（3，0）和C（4，6）；
（1）求抛物线的表达式；
（2）现将此抛物线先沿x轴方向向右平移6个单位，再沿y轴方向平移k个单位，若所得抛物线与x轴交于点D、E（点D在点E的左边），且使△ACD∽△AEC（顶点A、C、D依次对应顶点A、E、C），试求k的值，并注明方向．
（1）y=2x2﹣8x+6；（2）向下平移6个单位．
【解析】试题分析：（1）利用待定系数法直接求出抛物线的解析式；
（2）设出D，E坐标，根据平移，用k表示出平移后的抛物线解析式，利用坐标轴上点的特点得出m+n=16，mn=63﹣，进而利用相似三角形得出比例式建立方程即可求出k．
试题解析：【解析】
（1）∵抛物线过点A（1，0）、B（3，0），∴设抛物线的解析式为y=a（x... 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？
（1）y=﹣30x+2100．（2）每件售价定为55元时，每星期的销售利润最大，最大利润6750元．
（3）每星期至少要销售该款童装360件．
【解析】试题分析：（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．
（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．
（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．
试题解... 如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．
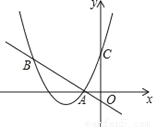
（1）抛物线解析式为y=x2+4x+3，一次函数解析式为y=﹣x﹣1；（2）由图象可知，满足（x+2）2+m≥kx+b的x的取值范围为x?﹣4或x≥﹣1．
【解析】（1）先利用待定系数法先求出m，再求出点B坐标，利用方程组求出太阳还是解析式．
（2）根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围．
【解析】
（1）∵抛物线y=（x+2）2+m经过点A（﹣1，0... 如图，已知抛物线y=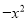
+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），
（1）求m的值及抛物线的顶点坐标．
（2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．
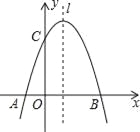
(1)m=2,(1,4)；(2)（1,2）.
【解析】试题分析：（1）首先把点B的坐标为（3，0）代入抛物线y=+mx+3，利用待定系数法即可求得m的值，继而求得抛物线的顶点坐标；
（2）首先连接BC交抛物线对称轴l于点P，则此时PA+PC的值最小，然后利用待定系数法求得直线BC的解析式，继而求得答案．
试题解析：（1）把点B的坐标为（3，0）代入抛物线y=+mx+3得：0=+3... 自主学习，请阅读下列解题过程．
解一元二次不等式：x2﹣5x＞0．
【解析】
设x2﹣5x=0，解得：x1=0，x2=5，则抛物线y=x2﹣5x与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x2﹣5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x2﹣5x＞0，所以，一元二次不等式x2﹣5x＞0的解集为：x＜0，或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
（1）上述解题过程中，渗透了下列数学思想中的 和 ．（只填序号）
①转化思想 ②分类讨论思想 ③数形结合思想
（2）一元二次不等式x2﹣5x＜0的解集为 ．
（3）用类似的方法解一元二次不等式：x2﹣2x﹣3＞0．
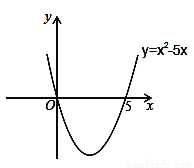
（1）①，③（2）0＜x＜5（3）x＜﹣1，或x＞3．
【解析】试题分析：（1）解题过程中，渗透了转化思想和数形结合思想；
（2）观察图象即可写出一元二次不等式：x2﹣5x＜0的解集；
（3）先设函数解析式，根据a的值确定抛物线的开口向上，再找出抛物线与x轴相交的两点，就可以画出抛物线，根据y＞0确定一元二次不等式x2﹣2x﹣3＞0的解集．
试题解析：【解析】
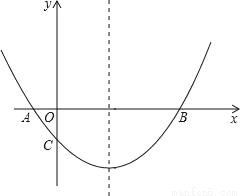
（1）上述... 如图，抛物线经过A（﹣1，0），B（5，0），C（0，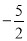 
）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
（1）y=x2﹣2x﹣；（2）P（2，﹣）；（3）点N的坐标为（4，﹣），（2+， ）或（2﹣， ）．
【解析】试题分析：本题考查的是二次函数综合题，涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识，在解答（3）时要注意进行分类讨论．（1）设抛物线的解析式为y=ax2+bx+c（a≠0），再把A（﹣1，0），B（5，0），C（0，）三点代入求出a、b、c... 下列说法错误的是（ ）
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等，另一组对边平行的四边形是平行四边形
D
【解析】一组对边相等，另一组对边平行不能判定四边形为平行四边形，故D选项错误.
故选D.