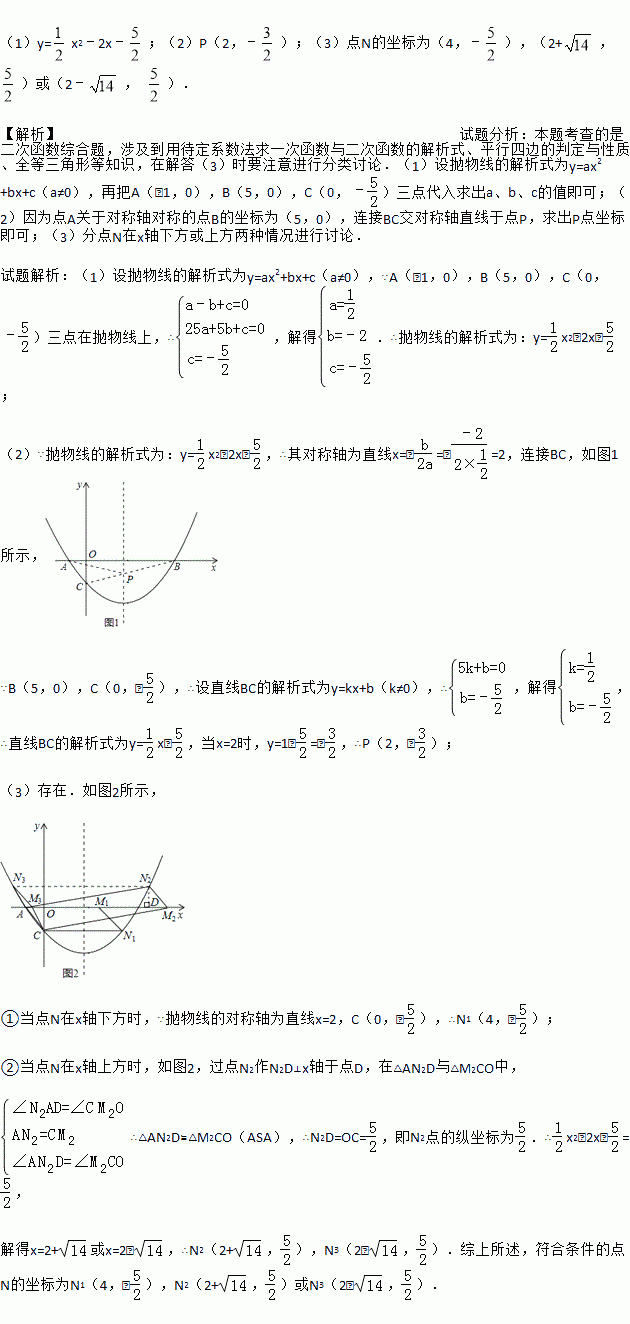��Ŀ����
��ͼ�������߾���A����1��0����B��5��0����C��0�� 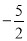 �����㣮
�����㣮
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�������һ��P��ʹPA+PC��ֵ��С�����P�����ꣻ
��3����MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��A��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�
 ��1��y=x2��2x������2��P��2����������3����N��������4����������2+�� ����2���� ����
��������������������⿼����Ƕ��κ����ۺ��⣬�漰���ô���ϵ������һ�κ�������κ����Ľ���ʽ��ƽ���ıߵ��ж������ʡ�ȫ�������ε�֪ʶ���ڽ��3��ʱҪע����з������ۣ���1���������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ٰ�A����1��0����B��5��0����C��0��������������a��b��c...
��1��y=x2��2x������2��P��2����������3����N��������4����������2+�� ����2���� ����
��������������������⿼����Ƕ��κ����ۺ��⣬�漰���ô���ϵ������һ�κ�������κ����Ľ���ʽ��ƽ���ıߵ��ж������ʡ�ȫ�������ε�֪ʶ���ڽ��3��ʱҪע����з������ۣ���1���������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ٰ�A����1��0����B��5��0����C��0��������������a��b��c...
��ͼ���ڡ�ABC�У���D��E��F�ֱ��DZ�AB��BC��CA�ϵ��е㣬��AB=6cm��AC=8cm�����ı���ADEF���ܳ����� cm��
 14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm.
14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm. ��ͼ��һ����5��ֽƬƴ�ɵ�ƽ���ı��Σ�����ֽƬ֮�以���ص�Ҳ��϶���������ŵ���ֱ��������ֽƬ�������ΪS1��������ֱ��������ֽƬ�������ΪS2���м�һ��������ֽƬ�����ΪS3�������ƽ���ı��ε����һ�����Ա�ʾΪ��������
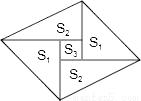
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
 A
����������������������ֱ�������ε�ֱ�DZ߳�Ϊa���м�С�����εı߳�Ϊb����������ֱ�������εı߳��ֱ�Ϊa-b��a+b������S1=��S2=��S3=��ƽ���ı��ε����=2S1+2S2+S3=++=2=4S1���ʴ�ѡA.
A
����������������������ֱ�������ε�ֱ�DZ߳�Ϊa���м�С�����εı߳�Ϊb����������ֱ�������εı߳��ֱ�Ϊa-b��a+b������S1=��S2=��S3=��ƽ���ı��ε����=2S1+2S2+S3=++=2=4S1���ʴ�ѡA. ��ͼ���ڡ�ABC�У���D��E�ֱ��DZ�AB��AC���е㣬AF��BC������Ϊ��F����ADE=30�㣬DF=4����BF�ij�Ϊ�� ��
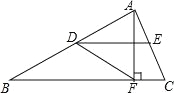
A��4 B��8 C��2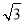 D��4
D��4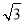
 D��
��������
�����������RT��ABF�У���AFB=90�㣬AD=DB��DF=4������ֱ��������б���������ʿɵ�AB=2DF=8������AD=DB��AE=EC���ɵ�DE��BC����ADE=��ABF=30�㣬����AF=AB=4���ɹ��ɶ����ɵ�BF=4����ѡD��
D��
��������
�����������RT��ABF�У���AFB=90�㣬AD=DB��DF=4������ֱ��������б���������ʿɵ�AB=2DF=8������AD=DB��AE=EC���ɵ�DE��BC����ADE=��ABF=30�㣬����AF=AB=4���ɹ��ɶ����ɵ�BF=4����ѡD�� һ������ε���Ǻ��������ڽǺ���ȣ���������( )
A. ������ B. �ı��� C. ����� D. ������
 B
���������������Ǻ�Ϊ���ڽǺ�Ϊ��
��
��
���Ըö����Ϊ�ı��Σ�
B
���������������Ǻ�Ϊ���ڽǺ�Ϊ��
��
��
���Ըö����Ϊ�ı��Σ� ƽ��ֱ������ϵxOy�У��Գ���ƽ����y��������߹���A��1��0����B��3��0����C��4��6����
��1���������ߵı���ʽ��
��2���ֽ�������������x�᷽������ƽ��6����λ������y�᷽��ƽ��k����λ����������������x�ύ�ڵ�D��E����D�ڵ�E����ߣ�����ʹ��ACD�ס�AEC������A��C��D���ζ�Ӧ����A��E��C��������k��ֵ����ע������
 ��1��y=2x2��8x+6����2������ƽ��6����λ��
�������������������1�����ô���ϵ����ֱ����������ߵĽ���ʽ��
��2�����D��E���꣬����ƽ�ƣ���k��ʾ��ƽ�ƺ�������߽���ʽ�������������ϵ���ص�ó�m+n=16��mn=63���������������������εó�����ʽ�������̼������k��
�����������������
��1���������߹���A��1��0����B��3��0�������������ߵĽ���ʽΪy=a��x...
��1��y=2x2��8x+6����2������ƽ��6����λ��
�������������������1�����ô���ϵ����ֱ����������ߵĽ���ʽ��
��2�����D��E���꣬����ƽ�ƣ���k��ʾ��ƽ�ƺ�������߽���ʽ�������������ϵ���ص�ó�m+n=16��mn=63���������������������εó�����ʽ�������̼������k��
�����������������
��1���������߹���A��1��0����B��3��0�������������ߵĽ���ʽΪy=a��x... ��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��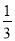 ��a��
��a��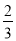 ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������
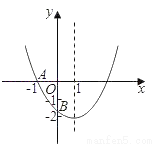
A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
 D
������������������١ߺ������ڷ������ϣ���a��0���߶Գ�����y���Ҳ࣬��ab��ţ�����������y�ύ����y�Ḻ���ᣬ��c��0����abc��0���ʢ���ȷ���ڡ�ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����ͼ����x�����һ������Ϊ��3��0�����൱x=2ʱ��y��0����4a+2b+c��0���ʢڴ��ۡ�ͼ����x�ύ�ڵ�A����1��0�����൱x=��1ʱ��y= =0����a��b+c=0����a=b��c...
D
������������������١ߺ������ڷ������ϣ���a��0���߶Գ�����y���Ҳ࣬��ab��ţ�����������y�ύ����y�Ḻ���ᣬ��c��0����abc��0���ʢ���ȷ���ڡ�ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����ͼ����x�����һ������Ϊ��3��0�����൱x=2ʱ��y��0����4a+2b+c��0���ʢڴ��ۡ�ͼ����x�ύ�ڵ�A����1��0�����൱x=��1ʱ��y= =0����a��b+c=0����a=b��c... ��ͼ���Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊֱ��x=1��������x��һ����ΪA��3��0��������ͼ���֪������ʽax2+bx+c��0�Ľ⼯��_____��
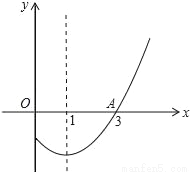
 ��1��x��3
��������������������ݶ��κ��������ʿɵã����κ�����x�����һ����������Ϊ(-1��0)������ݶ��κ�����ͼ��ɵã�����ʽ�Ľ⼯Ϊ.
��1��x��3
��������������������ݶ��κ��������ʿɵã����κ�����x�����һ����������Ϊ(-1��0)������ݶ��κ�����ͼ��ɵã�����ʽ�Ľ⼯Ϊ. ��ͼ����һ�����߹��ţ���ˮλ����ABλ��ʱ�����Ŷ���ˮ��2m��ˮ���4m��ˮ���½�1m��ˮ���Ϊ( )
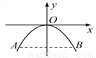
A. 5m B. 6m C. 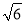 m D. 2
m D. 2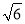 m
m
 D
�����������������������ͼ��ʾ������ϵ�����A������Ϊ��-2��-2�����躯����ϵʽΪ����-2=4a������a= -�����ԣ���y=-3ʱ�� ������ˮ���Ϊm����ѡ��D��
D
�����������������������ͼ��ʾ������ϵ�����A������Ϊ��-2��-2�����躯����ϵʽΪ����-2=4a������a= -�����ԣ���y=-3ʱ�� ������ˮ���Ϊm����ѡ��D��