设A、B两点关于直线MN轴对称,则_______垂直平分________.
直线MN 线段AB
【解析】∵A、B两点关于直线MN轴对称，
∴由轴对称的性质可得，直线MN垂直平分线段AB. 若直角三角形是轴对称图形,则其三个内角的度数分别为________.
90°45°45°
【解析】∵直角三角形是轴对称图形 ，
∴一定有两个角相等.
又∵直角三角形一定有一个角为90°，
∴相等的是两个锐角.
∵直角三角形的两个锐角互余，
∴每一个锐角为45°. 已知在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B',如图所示,则与线段BC相等的线段是____，与线段AB相等的线段是_______和_______,与∠B相等的角是________和_______,因此可得到∠B=________.
B′ C AB′ BB ′ ∠B′ ∠BAB′ 60°
【解析】∵以直线AC为对称轴,点B的对称点是B' ，
∴B′C=BC ， ∠B′CA=∠BCA=90°，AB′=AB=2BC，
∴AB′=AB=BB′，
∴∠B′=∠B=∠B′AB =60°. 如图，已知点A、B直线MN同侧两点， 点A’、A关于直线MN对称.连接A’B交直线MN于点P,连接AP.若A’B＝5cm，则AP+BP的长为________
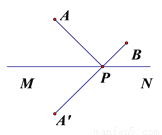
5cm
【解析】∵点A′、A关于直线MN对称，点P在对称轴MN上，
∴A′P、AP关于直线MN对称，
∴A′P=AP，
∴AP+BP= A′P+PB=A′B＝5cm. 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm. 找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.
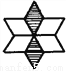
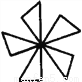
（1） (2) (3)
见解析
【解析】试题分析：本题考查了利用轴对称设计图案的知识,解答本题的关键是熟练掌握轴对称的性质.观察可知①是轴对称图形,先确定对称轴,然后找对应点、对应线段及对应角.
【解析】
第一个图形是轴对称图形，第二、三个图形是旋转对称图形.
如上图所示，若以EF为对称轴,则点A与点B、点M与点N、点C与点D等是对应点.线段AG与BH、CM与DN、PG与PH等是对应线段,∠A与∠B、... 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM， 求△ABC中AB边上的高h.
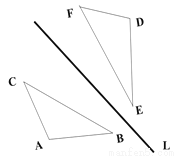
h=4cm
【解析】试题分析：本题思路的关键是利用轴对称图形的性质，得到AB =DE=3cm，然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF，
∴AB =DE=3cm，
∴h=6×2÷3=4cm. 小红想在卧室放一穿衣镜，能看到自己的全身像，那么她至少应买多高(宽度适当)的穿衣镜？
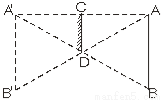
镜高至少为身高的一半
【解析】试题分析：设小红用线段AB表示，则A头部，通过镜子下沿D处可以看到自己的脚的映像，而根据轴对称的性质，可以通过镜子顶端C处看到自己的头部映像，因此，镜子调试至少需要自己身体的一半高度.
【解析】
由轴对称的性质得CA=CA′，
∵CD∥AB,
∴CD为△AA′B的中位线 ，
∴镜子高度至少为身高的一半． 下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗?(有几个字的笔划在对称轴上)
，
，
，
，
.
见解析
【解析】试题分析：根据汉字的对称结构来确定是哪个汉字，对于第一个图，思考可能是口或中，但是口没有那么扁平，故为中；第二个图左边应该也是一个木，这样原来的汉字应该是林；第三个图形，根据轴对称可以容易得到是一个南字；第四个从对称上来研究，应该左边下方也有一个点，再考虑对称轴上可能有笔画，容易得到是京字；第五个图，从对称可以得到右边有点、横、捺，可是不是我们所学过的汉字，再考虑对称轴上的笔... 如图，A与A′关于直线MN对称，P是BA′与MN的交点.若P1为直线MN上任意一点（不与P重合），连结AP1、BP1，试说明 AP1+BP1>AP+BP.
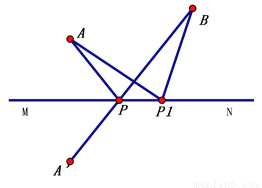
见解析
【解析】试题分析：由三角形三条边的关系可得A′P1+BP1>A′B，再由轴对称的性质可得AP1=A′P1，然后通过等量代换可证明结论.
【解析】
如图，连结AP1，则在△A′P1B中，有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称，
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得：AP=...