连续平移只改变图形的那方面，没有改变图形的哪几方面？
连续平移只改变图形的位置，没有改变图形的形状、大小.
【解析】试题分析：根据平移的特征回答即可.
试题解析：
根据平移的特征可以得出连续平移只改变图形的位置，没有改变图形的 形状、大小. 如图所示，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠A等于( )
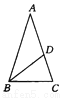
A. 30° B. 40° C. 45° D. 36°
D
【解析】∵AD＝BD，
∴∠A＝∠ABD，
∴∠BDC＝2∠A.
∵BD＝BC，
∴∠C＝∠BDC＝2∠A．
∵AB＝AC，
∴∠ABC＝∠C＝2∠A，
由三角形内角和定理，得∠A+2∠A+2∠A＝180°，
即∠A＝36°．
故选D. 在等腰梯形ABCD中，∠ABC＝2∠ACB，BD平分∠ABC，AD∥BC，如图所示，则图中的等腰三角形有( )
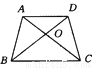
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】∵AD∥BC，∠ADB=30°，
∴∠CBD=∠ADB=30°.
∵ABCD为等腰梯形，
∴∠ABC=∠DCB=60°，则∠BAD=∠ABC-∠CBD=30°，
∴△ABD为等腰三角形.
同理可证△ACD为等腰三角形，
∵∠ABO=∠DCO=30°，∠AOB=∠DOC，AB=CD，
∴△AOB≌△DOC，
∴AO=DO，BO=CO，... 如图，在□ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE等于（ ）
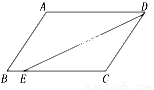
A. 2cm B. 4cm C. 6cm D. 8cm
A
【解析】试题分析：由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA=∠DEC，而DE平分∠ADC，进一步推出∠EDC=∠DEC，在同一三角形中，根据等角对等边得CE=CD=6，则BE可求BE=BC-EC=8-6=2．
故选：A． 下面几种三角形：
①有两个角为60°的三角形；
②三个外角都相等的三角形；
③一条边上的高也是这条边上的中线的三角形；
④有一个角为60°的等腰三角形．
其中是等边三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】对于①，有两个角为60°的三角形为等边三角形，故①正确；
对于②，三个外角都相等的三角形为等边三角形，故②正确；
对于③，一条边上的高也是这条边上的中线的三角形有可能是等腰三角形或等边三角形，故③错误；
对于④，有一个角为60° 的等腰三角形为等边三角形，故④正确.
综上，①②④所述为等边三角形.
故选B. 用反证法证明命题“三角形中至少有一个内角大于或等于60°”，第一步应假设 。
三角形的三个内角都小于60°．
【解析】
试题分析：熟记反证法的步骤，直接填空即可．
试题解析：第一步应假设结论不成立，即三角形的三个内角都小于60°． 等腰三角形的顶角α＞90°，如果过其顶角的顶点作一条直线将这个等腰三角形分 成了两个等腰三角形，那么α的度数为________．
108°
【解析】如图，
∵AB=AC，BD=AD，AC=CD，
∴∠1=∠B，∠2=∠4，∠B=∠C，
∵∠4=∠1+∠B=2∠B=2∠C，
∴∠2=∠4=2∠C，
∵∠2+∠4+∠C=180°，
∴5∠C=180°，
∴∠C=36°，
∴α=∠BAC=180°-2∠C=108°． 如图，四边形ABCD的对角线AC与BD相交于O点，∠1=∠2，∠3=∠4．
求证：(1)△ABC≌△ADC；(2)BO=DO．
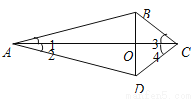
(1)、证明过程见解析；(2)、证明过程见解析
【解析】试题分析：(1)、根据∠1=∠2，AC=AC，∠3=∠4得到△ABC和△ADC全等；(2)、根据全等得出AB=AD，然后结合∠1=∠2，AO=AO得出△ABO和△ADO全等，从而得到BO=DO.
试题解析：(1)、在△ABC和△ADC中∴△ABC≌△ADC．
(2)、∵△ABC≌△ADC ∴AB=AD 在△ABO和△ADO中... 文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
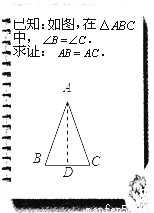
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
（1）作辅助线不能同时满足两个条件；（2）证明见解析.
【解析】试题分析：（1）线段BC的中垂线可以直接作出的，不需要附带“过点A作”；
（2）根据已知条件利用AAS可证△ABD≌△ACD，得出AB=AC．
试题解析：（1）作辅助线不能同时满足两个条件；
（2）证明：作△ABC的角平分线AD．
∴∠BAD=∠CAD，
在△ABD与△ACD中，
∴△ABD≌... 四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
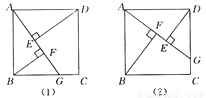
EF＝AF－BF △ABF≌△DAE EF＝BF－AF
【解析】试题分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．
(1) 证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，
∴∠BAF+∠DAE＝90°．
...