小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
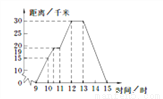
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
 (1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看...
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 某移动通信公司开设了两种通信业务,“全球通”:使用时首先缴50元月租费,然后每通话1分钟,付话费0.4元;“动感地带”:不缴月租费,每通话1分钟,付话费0.6元(本题的通话均指市内通话).若一个月通话x分钟,两种方式的费用分别为y1元和y2元.
(1)写出y1,y2与x之间的关系式;
(2)一个月内通话多少分钟,两种方式费用相同?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算些?
 【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解...
【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解... 近期,大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)以前在两岸未直接通航时,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,一次进货最多只能是多少千克?
 (1)y=50+2x;(2) 1518千克
【解析】试题分析:(1)根据表格发现每下调一元,多销售2kg,由此即可解决问题.
(2)当x=30时,代入解析式求出销量,根据利润=售价-进价就可以求出结论;
(3)根据凤梨的保存时间和运输路线的影响,凤梨的销售时间最多是23天.要想使售价不低于30元/千克,就必须在最多23天内卖完,当售价为30元/千克时,销售量已经由(2)求出,因此...
(1)y=50+2x;(2) 1518千克
【解析】试题分析:(1)根据表格发现每下调一元,多销售2kg,由此即可解决问题.
(2)当x=30时,代入解析式求出销量,根据利润=售价-进价就可以求出结论;
(3)根据凤梨的保存时间和运输路线的影响,凤梨的销售时间最多是23天.要想使售价不低于30元/千克,就必须在最多23天内卖完,当售价为30元/千克时,销售量已经由(2)求出,因此... (3分)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.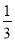 B.3 C.
B.3 C.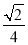 D.
D.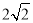
 D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D.
D.
【解析】
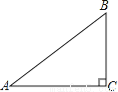
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )
A. 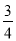 B.
B. 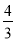 C.
C. 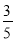 D.
D. 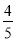
 C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A.
C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A. 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
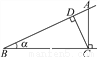
A. 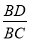 B.
B. 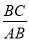 C.
C. 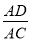 D.
D. 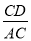
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C. 已知sin6°=a,sin36°=b,则sin26°=( )
A. a2 B. 2a C. b2 D. b
 A
【解析】∵sin6°=a,
∴=a2.
故选:A.
A
【解析】∵sin6°=a,
∴=a2.
故选:A. 在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B.都缩小两倍 C.不变 D.都扩大四倍
 C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C.
C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C. △ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A. bcosB=c B. csinA=a C. atanA=b D. tanB=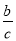
 B
【解析】∵a2+b2=c2,
∴△ABC是直角三角形,且∠C=90°,
∴sinA=即csinA=a,
∴B选项正确.
故选B.
B
【解析】∵a2+b2=c2,
∴△ABC是直角三角形,且∠C=90°,
∴sinA=即csinA=a,
∴B选项正确.
故选B. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A. b=atanB B. a=ccosB C. c=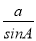 D. a=bcosA
D. a=bcosA
 D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.