比较下列三角函数值的大小:sin40°___________sin50°
 <
【解析】根据当0<α<90°,sinα随α的增大而增大即可得到:
∵40°<50°,
∴sin40°<sin50°.
故答案为<.
<
【解析】根据当0<α<90°,sinα随α的增大而增大即可得到:
∵40°<50°,
∴sin40°<sin50°.
故答案为<. 比较下列三角函数值的大小:sin40°______cos40°(选填“>”、“=”、“<”)
 【解析】∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40°
【解析】∵cos40°=sin50°,正弦值随着角的增大而增大,
又∵40°<50°,
∴sin40°<cos40° 如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为 .
 【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以.
【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以. 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为: 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
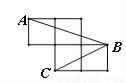
 【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值.
【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值. Rt△ABC中,∠C=90°,AB=10,BC=8,求cosB的值.
 【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析:
∵∠C=90°,AB=10,BC=8,
∴cosB=
故答案为:
【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析:
∵∠C=90°,AB=10,BC=8,
∴cosB=
故答案为: 在Rt△ABC中,∠C=90°,如果AC:BC=3:4,求cosA的值.
 【解析】分析:根据题意设AC=3x,BC=4x,故AB=5x,进而利用锐角三角函数关系求出答案.
本题解析:
∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
故答案为:
【解析】分析:根据题意设AC=3x,BC=4x,故AB=5x,进而利用锐角三角函数关系求出答案.
本题解析:
∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
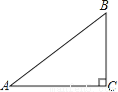
故答案为: 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )
A. 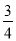 B.
B. 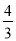 C.
C. 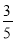 D.
D. 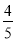
 C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A.
C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
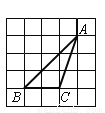
故选A. 如图所示,△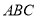 的顶点是正方形网格的格点,则sin
的顶点是正方形网格的格点,则sin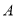 的值为( )
的值为( )
A. 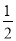 B.
B. 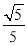 C.
C. 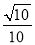 D.
D. 
 B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键.
B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键. 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
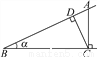
A. 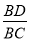 B.
B. 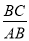 C.
C. 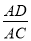 D.
D. 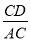
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.