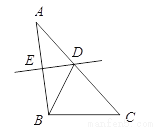
△ABC中，AB = 5，AC = 6，BC = 4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）
A. 8 B. 9 C. 10 D. 11
C
【解析】试题分析：由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC． ∵ED是AB的垂直平分线， ∴AD=BD，
∵△BDC的周长=DB+BC+CD， ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10． 如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
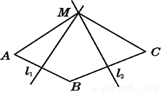
A. AM>CM B. AM=CM C. AM<CM D. 无法确定
B
【解析】首先连接BM，然后根据l1是线段AB的垂直平分线判定AM=BM；类似的方法可得BM与CM的关系，最后利用等量代换即可解答本题.
【解析】
如图所示：连接BM，
∵l1是线段AB的垂直平分线，
∴AM=BM，
∵l2是线段BC的垂直平分线，
∴BM=CM，
∴AM=CM.
故选B. 如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于
AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（ ）
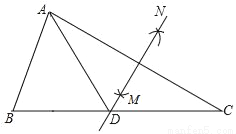
A. 65° B. 60° C. 55° D. 45°
A
【解析】分析：根据线段垂直平分线的性质得到AD=DC，根据等腰三角形的性质得到∠C=∠DAC，
求得∠DAC=30°，根据三角形的内角和得到∠BAC=95°，即可得到结论．
详解：由题意可得：MN是AC的垂直平分线，则AD=DC，故∠C=∠DAC．
∵∠C=30°，∴∠DAC=30°．
∵∠B=55°，∴∠BAC=95°，∴∠BAD=∠BAC﹣∠CAD=65°．
... 如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为( )
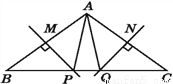
A. 12 cm B. 6 cm C. 8 cm D. 无法确定
B
【解析】由MP、NQ分别垂直平分AB、AC，根据线段垂直平分线的性质，可得BP=AP，CQ=AQ，继而求得△APQ的周长等于BC．
【解析】
∵MP、NQ分别垂直平分AB、AC，
∴BP=AP，CQ=AQ，
∵BC=6cm，
∴△APQ的周长为：AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B. 如图,已知直线l是AB的垂直平分线,M是直线l上的一点,D,E是AB上不同的点,则AM=BM吗?MD=ME吗?
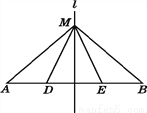
AM=BM,无法判断MD是否等于ME.
【解析】由M在线段AB的垂直平分线l上，根据“线段的垂直平分线上任意一点，到线段两端点的距离相等”即可判断AM=BM成立；根据直线l不一定是DE的垂直平分线，则无法判断MD与ME的大小关系.
【解析】
∵l是AB的垂直平分线，
∴AM=BM．
由于D、E是AB上任意两点，所以MD不一定等于ME，只有当l经过DE的中点时，MD=ME．... 如图所示,AB-AC=2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,
求AB和AC的长.
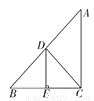
AB=8,AC=6
【解析】试题分析：根据线段垂直平分线性质求出BD=DC，根据三角形周长求出AB+AC=12cm，根据已知得出AC=AB-2cm，即可求出答案．
试题解析：
∵DE垂直平分BC,
∴BD=CD.
∴△ACD的周长=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
解方程组
得
∴AC=6cm，AB=8cm. 如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.连接AB,交ON于D点,交OM于C点,若AB长为15 cm,求△PCD的周长.
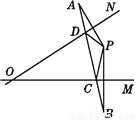
15 cm.
【解析】由点P与点A关于直线ON对称，点P与点B关于直线OM对称可得：ON垂直平分AP，OM垂直平分BP；根据垂直平分线的性质可得DA=DP，CP=CB，通过等量代换得到△PCD的周长与AB的数量关系，即可求解.
【解析】
∵点P与点A关于直线ON对称，点P与点B关于直线OM对称，
∴ON垂直平分AP，OM垂直平分BP，
∴DA=DP，CP=CB，
∴... 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
求证：（1）FC＝AD；
（2）AB＝BC＋AD．
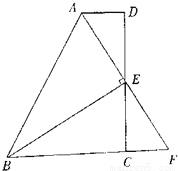
（1）证明见解析；（2）证明见解析.
【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．
（2）根据线段垂直平分线的性质判断出AB=BF即可．
证明：（1）∵AD∥BC（已知），
∴∠ADC=∠ECF（两直线平行，内错角相等），
∵E是CD的中点（已知），
∴DE=EC（中点... 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
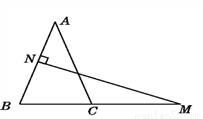
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
(1) 20°；(2) 35°；
(3)规律:∠NMB=∠A.
【解析】（1）根据等边对等角，由AB=AC可得到∠ABM=∠ACB，再结合已知∠A的度数，即可求出∠NMB的度数；
（2）仿照第（1）问的求解过程即可得到∠NMB的度数；
（3）结合上述两问的解答，即可发现∠NMB和∠A之间的大小关系，然后仿照上述解答过程进行验证即可.
【解析】
（1）∵AB=AC，
... 锐角三角形中，最大角α的取值范围是（ ）
A. 0°< α < 90° B. 60°< α < 180° C. 60°< α < 90° D. 60°≤α < 90°
D
【解析】试题分析：根据三角形的内角和定理，又α是最大角，得：3α≥180°，即α≥60°，故最大角α的取值范围是60°≤α＜180度．