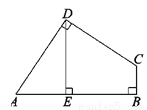
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DE⊥AB于点E,若四边形ABCD的面积为16,则DE=__.
 4
【解析】试题解析:过点D作BC的垂线,交BC的延长线于F,
又
∴≌,
∴,
四边形ABCD的面积=正方形DEBF的面积=16,
∴DE=4.
故答案为:4.
4
【解析】试题解析:过点D作BC的垂线,交BC的延长线于F,
又
∴≌,
∴,
四边形ABCD的面积=正方形DEBF的面积=16,
∴DE=4.
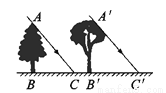
故答案为:4. 如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
 6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),...
6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
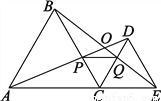
∴AB=A′B′=6米 (全等三角形的对应边相等),... 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是___________.
 ①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC...
①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC... 已知△ABC.求作:△A′B′C′,使△A′B′C′≌△ABC.
 作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A...
作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A... 如图,已知在△ABC中,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与 (∠C-∠B)的关系,并说明理由.
(∠C-∠B)的关系,并说明理由.
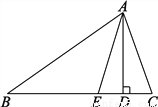
 ∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC,
∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC, 如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
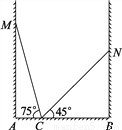
 a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
...
a米.
【解析】试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
... 如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,∠P=∠Q=45°,将一三角尺的直角顶点放在点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明:MA=MB.
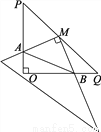 +
+
 说明见解析
【解析】试题分析:过点M作ME⊥PO,MF⊥QO,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得再利用“角边角”证明和全等,根据全等三角形对应边相等即可证明;
试题解析:过点M作ME⊥PO,MF⊥QO,
∴∠PEM=∠QFM=90°,又∵∠P=∠Q=45°,
∴∠PME=∠QMF=45°,∠EMF=90°,
又∵P...
说明见解析
【解析】试题分析:过点M作ME⊥PO,MF⊥QO,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得再利用“角边角”证明和全等,根据全等三角形对应边相等即可证明;
试题解析:过点M作ME⊥PO,MF⊥QO,
∴∠PEM=∠QFM=90°,又∵∠P=∠Q=45°,
∴∠PME=∠QMF=45°,∠EMF=90°,
又∵P... 下列说法中,正确的是( )
A. 不可能事件发生的概率为0
B. 随机事件发生的概率为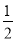
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
 A
【解析】试题分析:不可能事件发生的概率为0,故A正确;
随机事件发生的概率为在0到1之间,故B错误;
概率很小的事件也可能发生,故C错误;
投掷一枚质地均匀的硬币100次,正面向上的次数为50次是随机事件,D错误;
故选A.
A
【解析】试题分析:不可能事件发生的概率为0,故A正确;
随机事件发生的概率为在0到1之间,故B错误;
概率很小的事件也可能发生,故C错误;
投掷一枚质地均匀的硬币100次,正面向上的次数为50次是随机事件,D错误;
故选A. 如图,在平行四边形纸片上作随机扎针试验,针头扎在阴影区域内的概率为( )

A. 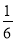 B.
B. 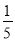 C.
C. 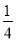 D.
D. 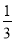
 C
【解析】根据概率公式可得,随机扎针,扎在阴影部分区域的概率= = ,故选C.
C
【解析】根据概率公式可得,随机扎针,扎在阴影部分区域的概率= = ,故选C. 2014年3月,YC市举办了首届中学生汉字听写大会,从甲、乙、丙、丁4套题中随机抽取一套训练,抽中甲的概率是( )
A. 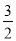 B.
B. 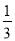 C.
C. 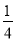 D.
D. 
 C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.
C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.