如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
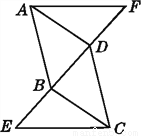
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
(1)AD∥BC；(2)BF=DE
【解析】试题分析：（1）由“已知全等三角形的对应角相等”推知∠ADF=∠CBE，则等角的补角相等，即内错角∠ADB=∠CBD，则易证得AD∥BC；
（2）由“已知全等三角形的对应边相等”推知BE=DF，则根据等式的性质得到BE+BD=DF+BD，即BF=DE．
试题解析: (1)AD∥BC.理由如下：
∵△ADF≌△CBE，
∴∠A... 如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
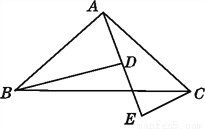
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
（1）见解析；（2）∠ADB=90°
【解析】试题分析：（1）根据全等三角形的性质求出BD=AE，AD=CE，代入求出即可；
（2）根据全等三角形的性质求出∠E=∠BDA=90°，推出∠BDE=90°，根据平行线的判定求出即可．
试题解析: (1)∵△BAD≌△ACE，
∴BD=AE，AD=CE，
∴BD=AE=AD+DE=CE+DE，
即BD=DE+CE；
... 如图，木工师傅在做完门框后，为防止变形常常象图中所示那样钉上两条斜拉的木条（图中的AB，CD两根木条），这样做是运用了三角形的（ ）
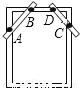
A. 全等性 B. 灵活性 C. 稳定性 D. 对称性
C
【解析】三角形具有稳定性，其他多边形不具有稳定性，把多边形分割成三角形则多边形的形状就不会改变，故这样做是运用了三角形的稳定性.
故选：C. 如图，AB=AC，BD=CD，则△ABD≌△ACD的依据是（ ）
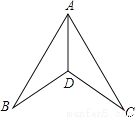
A. SSS B. SAS C. AAS D. HL
A
【解析】在△ABD和△ACD中，
，
∴△ABD和△ACD（SSS）；
故选：A. 如图，AB=CD，AD=CB，那么下列结论中错误的是（ ）
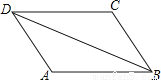
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
B
【解析】∵在△ABD和△CDB中，
，
∴△ABD≌△CDB，
∴∠ADB=∠CBD，∠ABD=∠CDB，∠A=∠C
∴AD∥BC，AB∥CD，
∴A、C、D选项正确.
故选：B. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
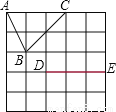
A. 2个 B. 4个 C. 6个 D. 8个
B
【解析】如图，根据题意，运用SSS可得与△ABC全等的三角形有4个，线段DE的上方和下方各有两个符合的点，共4个.
故选：A. 如图，AB∥CD，AD∥BC；则图中的全等三角形共有（ ）
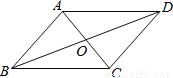
A. 5对 B. 4对 C. 3对 D. 2对
B
【解析】∵AB∥CD，AD∥BC，
∴四边形ABCD为平行四边形，
∴AB=CD，AD=BC，AO=CO，BO=DO，EO=FO，∠DAO=∠BCO，
又∠AOB=∠COD，∠AOD=∠COB，∠AOE=∠COF，
∴△AOB≌△COD（SSS），△AOD≌△COB（SSS），△ABC≌△CDA（SSS），△ABD≌△CDB（SSS）.
故图中的全等三角形共... 如图，AD=BC，DC=AB，AE=CF，找出图中的一对全等三角形，并说明你的理由。
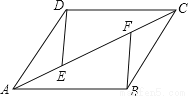
△ABC≌△CDA
【解析】试题分析：全等三角形之一是△ABC≌△CDA，理由是根据AB=DC，AD=BC，AC=AC，根据全等三角形的判定定理SSS推出即可．
试题解析：△ABC≌△CDA．
理由是：在△ABC和△CDA中，
∵
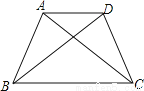
∴△ABC≌△CDA（SSS）. 如图，已知AB=CD，AC=BD，说明AD∥BC。
证明见解析
【解析】试题分析：由SSS证明△ABC≌△DCB，得出对应角相等∠ACB=∠DBC，同理：∠ADB=∠DAC，由三角形外角关系证出∠DAC=∠ACB，即可得出AD∥BC．
试题解析：在△ABC和△DCB中，
，
∴△ABC≌△DCB（SSS），
∴∠ACB=∠DBC，
同理：∠ADB=∠DAC，
∵∠ACB+∠DBC=∠ADB+∠DAC，
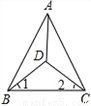
... 已知在△ABC中，∠ABC=∠ACB，∠1=∠2，求证：AD平分∠BAC。
证明见解析
【解析】试题分析：易证AB=AC和BD=CD，即可证明△ABD≌△ACD，可得∠BAD=∠CAD，即可解题．
试题解析：∵∠ABC=∠ACB，
∴AB=AC，
∵∠1=∠2，
∴BD=CD，
在△ABD和△ACD中，
，
∴△ABD≌△ACD（SSS），
∴∠BAD=∠CAD，
∴AD平分∠BAC.