0 319914 319922 319928 319932 319938 319940 319944 319950 319952 319958 319964 319968 319970 319974 319980 319982 319988 319992 319994 319998 320000 320004 320006 320008 320009 320010 320012 320013 320014 320016 320018 320022 320024 320028 320030 320034 320040 320042 320048 320052 320054 320058 320064 320070 320072 320078 320082 320084 320090 320094 320100 320108 366461
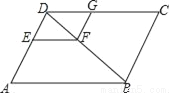
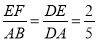 , 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.
, 得到AB的长,根据平行四边形的性质求出CD,根据平行线分线段成比例定理得到比例式,计算即可.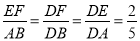 ,又EF=4,
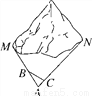
,又EF=4,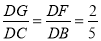 ,
,
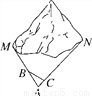
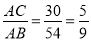 ,
, 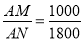 =
=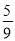 ,∴
,∴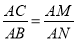 ,又∵∠A=∠A,
,又∵∠A=∠A,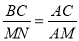 ,即
,即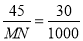 ,
,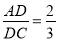 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.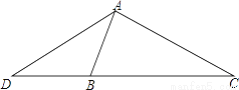
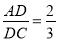 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.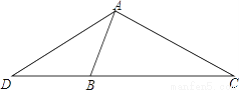
 ,
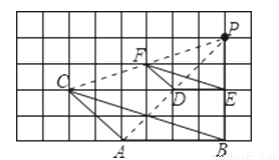
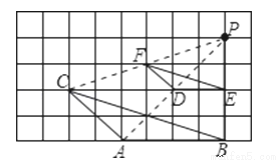
,
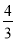 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).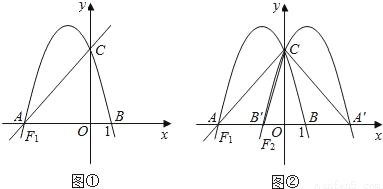
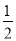 的相反数是( )
的相反数是( )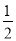 C. ﹣2 D. ﹣
C. ﹣2 D. ﹣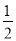

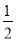 B.
B. 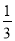 C.
C. 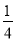 D.
D. 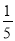
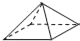
 B.
B.  C.
C.  D.
D. 