0 319328 319336 319342 319346 319352 319354 319358 319364 319366 319372 319378 319382 319384 319388 319394 319396 319402 319406 319408 319412 319414 319418 319420 319422 319423 319424 319426 319427 319428 319430 319432 319436 319438 319442 319444 319448 319454 319456 319462 319466 319468 319472 319478 319484 319486 319492 319496 319498 319504 319508 319514 319522 366461
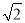 ;
;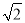 时,原式=2+2=4.
时,原式=2+2=4.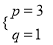 ;(2)x2-2px+3q不是完全平方式.理由见解析.
;(2)x2-2px+3q不是完全平方式.理由见解析.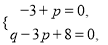
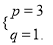
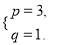 代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
代入x2-2px+3q,得x2-2px+3q=x2-6x+3.

 =________;
=________;  =________.
=________.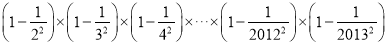
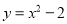 的顶点坐标为( )
的顶点坐标为( )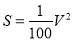 ,一辆车速为100km/h的汽车,刹车距离是 ( )
,一辆车速为100km/h的汽车,刹车距离是 ( )
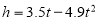 (的单位:秒,
(的单位:秒,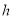 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
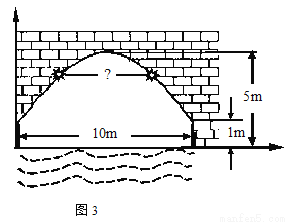
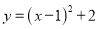 的最小值是____。
的最小值是____。