题目内容
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
【解析】
设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
乘法公式的探究及应用.
探究问题
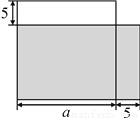
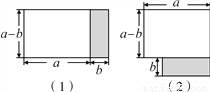
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.


(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
 =________;
=________;  =________.
=________.
拓展运用:
(5)计算: 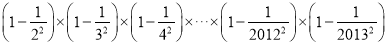


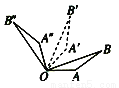
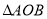 的顶点
的顶点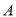 (
(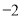 ,0)、
,0)、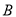 (
(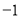 ,1)。将
,1)。将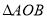 绕点O顺时针旋转
绕点O顺时针旋转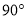 后,点
后,点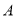 、
、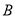 分别落在
分别落在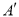 、
、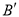 .
.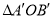 ;
;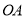 所扫过的图形的面积.
所扫过的图形的面积.