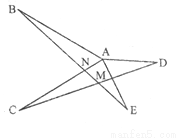
已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)
2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.
先化简,再求值: 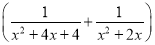 ÷
÷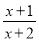 ,其中x=3.
,其中x=3.
解方程: 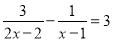
计算:
(1)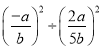 ·
·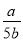
(2)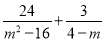
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)
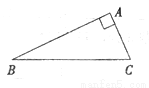
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
(1)AD=BE ;(2)详见解析. 【解析】试题分析:(1)根据基本作图,作一条线段等于已知线段的作图方法就可以作出图形; (2)延长AC到点F,使CF=AF,连接BF,证明△ACD≌△FCB,就有AD=FB,进而得出AE=AF,就可以得出BE=BF,从而结论AD=BE. 试题解析:(1)由题意,得作图如下: (2)延长AC到点F,使CF=AF,连接BF, 在△AC...已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.

先化简,再求值: 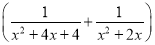 ÷
÷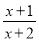 ,其中x=3.
,其中x=3.
解方程: 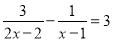
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
阅读下列材料:
(1)解方程: 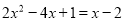
【解析】
方程化为: 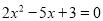 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=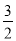 或x=1.
或x=1.
∴方程的根为: 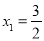 ,
, 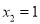 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 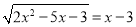 ;
;
(2)若方程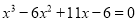 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.

先化简,再求值: 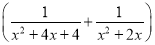 ÷
÷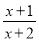 ,其中x=3.
,其中x=3.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
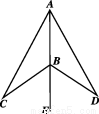
已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=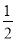 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;
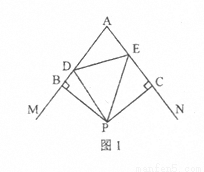
(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。
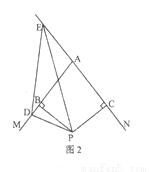
阅读下列材料:
(1)解方程: 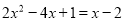
【解析】
方程化为: 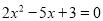 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=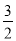 或x=1.
或x=1.
∴方程的根为: 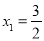 ,
, 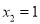 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 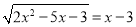 ;
;
(2)若方程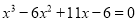 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.

- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
C 【解析】试题解析:∵x(x-3)=4, ∴x2-3x-4=0, ∴(x-4)(x+1)=0, ∴x-4=0或x+1=0, ∴x1=4,x2=-1. 故选C.已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=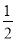 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

阅读下列材料:
(1)解方程: 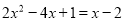
【解析】
方程化为: 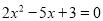 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=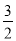 或x=1.
或x=1.
∴方程的根为: 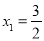 ,
, 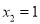 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 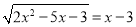 ;
;
(2)若方程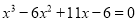 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,几何体的左视图是( )
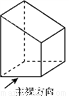

A. (A) B. (B) C. (C) D. (D)
C 【解析】从左面看所得到的图形,比较即可. 如图,几何体的左视图是. 故选C.一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=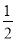 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

阅读下列材料:
(1)解方程: 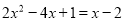
【解析】
方程化为: 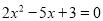 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=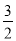 或x=1.
或x=1.
∴方程的根为: 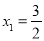 ,
, 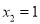 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 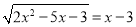 ;
;
(2)若方程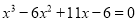 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
A 【解析】试题解析: ∵AC⊥BD,四边形ABCD是平行四边形, ∴平行四边形ABCD是菱形,不能推出四边形ABCD是矩形,∴①错误; ∵四边形ABCD是平行四边形, ∴平行四边形ABCD是矩形,∴②正确; ∵AB=BC,四边形ABCD是平行四边形, ∴平行四边形ABCD是菱形,不能推出四边形ABCD是矩形,∴③错误; ∵四边形ABCD是平行四边形...如图,几何体的左视图是( )


A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=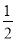 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

阅读下列材料:
(1)解方程: 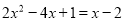
【解析】
方程化为: 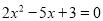 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=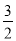 或x=1.
或x=1.
∴方程的根为: 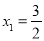 ,
, 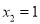 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 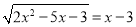 ;
;
(2)若方程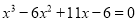 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 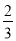 B.
B. 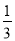 C.
C. 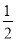 D.
D. 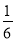
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )


A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=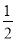 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

阅读下列材料:
(1)解方程: 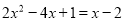
【解析】
方程化为: 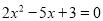 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=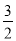 或x=1.
或x=1.
∴方程的根为: 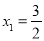 ,
, 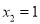 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 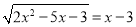 ;
;
(2)若方程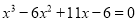 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为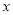 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 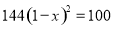 B.
B. 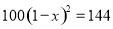
C. 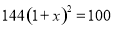 D.
D. 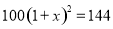
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 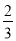 B.
B. 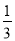 C.
C. 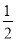 D.
D. 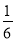
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )


A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=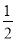 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
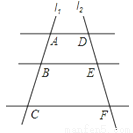
A. 4 B. 5 C. 6 D. 8
D 【解析】试题解析:∵AD∥BE∥CF, ∴,即, 解得,EF=6, ∴DF=DE+EF=2+6=8. 故选D.砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为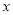 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 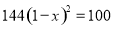 B.
B. 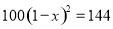
C. 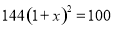 D.
D. 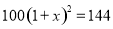
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 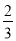 B.
B. 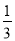 C.
C. 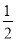 D.
D. 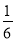
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )


A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧