题目内容
阅读下列材料:
(1)解方程: 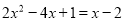
【解析】
方程化为: 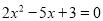 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=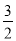 或x=1.
或x=1.
∴方程的根为: 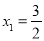 ,
, 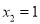 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 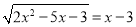 ;
;
(2)若方程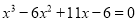 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
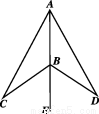
已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)
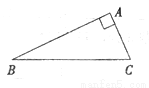
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【解析】
(1)AD与BE的大小关系是________________.
(2)证明:
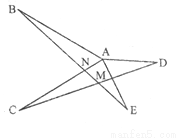
查看答案已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)
2017年9月17日,金秋的北京,我校初二全体同学到距学校30千米的房山农业职业学院,参加为期一周的学农劳动。同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往,结果和同学们同时到达了农职院。已知李老师开的私家车的速度是大巴车速度的1.2倍,求大巴车和李老师开的私家车的速度分别是多少?
查看答案如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.
先化简,再求值: 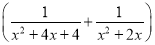 ÷
÷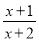 ,其中x=3.
,其中x=3.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知x≠1,(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)根据以上式子计算:
①(1-2)×(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=____________;
②(a-b)(a2+ab+b2)=____________;
③(a-b)(a3+a2b+ab2+b3)=____________.
(1)①-63;②2n+1-2;③x100-1.(2)①a2-b2;②a3-b3;③a4-b4 【解析】试题分析:(1)根据题意易得(1-x)(1+x+x2+…+xn)=1-xn+1; 利用猜想的结论得到①(1-2)(1+2+22+23+24+25)=1-26=1-64=-63; ②先变形2+22+23+24+…+2n=2(1+2+22+23+24+…+2n-1)=-2(1-2)...一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
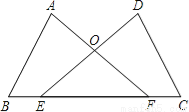
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.
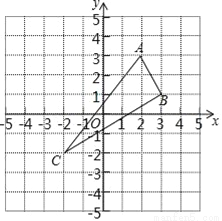
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案先化简,再求值: 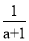 ﹣
﹣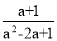 ÷
÷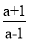 ,其中a=
,其中a=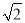 .
.
(1)计算4(x+1)2﹣(2x﹣5)(2x+5).
(2)解方程: 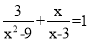 .
.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
无理数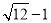 的大小在以下两个整数之间( )
的大小在以下两个整数之间( )
A. 1与2 B. 2与3 C. 3与4 D. 4与5
B 【解析】∵, ∴,即, ∴无理数的大小在2与3之间. 故选B.下列各组线段为边作三角形,不能构成直角三角形的是 ( )
A. 2 , 3 , 4 B. 1, 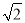 ,
, 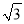 C. 5 , 12 , 13 D. 9, 40 , 41
C. 5 , 12 , 13 D. 9, 40 , 41
下列式子正确的是( )
A. 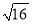 =±4 B. ±
=±4 B. ±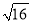 =4 C.
=4 C. 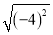 =-4 D. ±
=-4 D. ±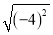 =±4
=±4
下列二次根式中的最简二次根式是 ( )
A. 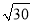 B.
B. 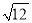 C.
C. 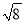 D.
D. 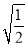
在实数0.333…,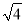 ,
, 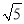 ,-π,3.1415,2.010010001…(相邻两个1之间0的个数逐渐增加)中,无理数有( )
,-π,3.1415,2.010010001…(相邻两个1之间0的个数逐渐增加)中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
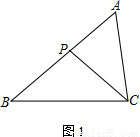
查看答案在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=AP·AB;
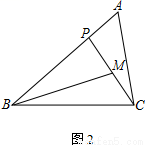
(2)若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
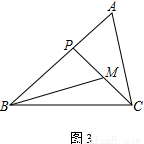
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
5 【解析】试题分析:根据根与系数的关系可知m+n=﹣2,又知m是方程的根,所以可得m2+2m﹣7=0,最后可将m2+3m+n变成m2+2m+m+n,最终可得答案. ∵设m、n是一元二次方程x2+2x﹣7=0的两个根, ∴m+n=﹣2, ∵m是原方程的根, ∴m2+2m﹣7=0,即m2+2m=7, ∴m2+3m+n=m2+2m+m+n=7﹣2=5 考点:根与系数的关系 ...如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
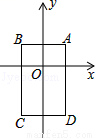
A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为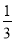 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
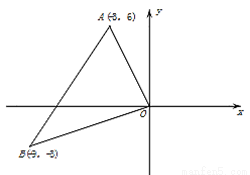
A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
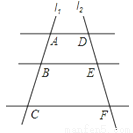
A. 4 B. 5 C. 6 D. 8
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 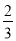 B.
B. 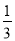 C.
C. 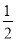 D.
D. 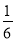
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )
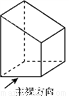

A. (A) B. (B) C. (C) D. (D)
查看答案一元二次方程x(x-3)=4的解是( )
A. 1 B. 4 C. -1或4 D. 1或-4
查看答案已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=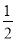 ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;
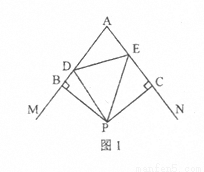
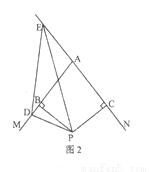
(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。
阅读下列材料:
(1)解方程: 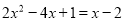
【解析】
方程化为: 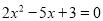 .
.
即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=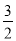 或x=1.
或x=1.
∴方程的根为: 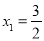 ,
, 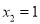 .
.
(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程: 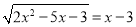 ;
;
(2)若方程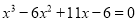 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
先化简,再求值: 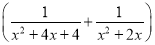 ÷
÷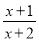 ,其中x=3.
,其中x=3.
解方程: 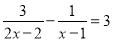
计算:
(1)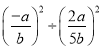 ·
·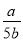
(2)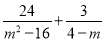
分解因式:
(1)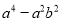
(2)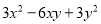
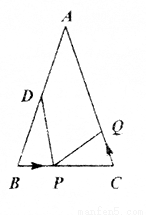
如图,在△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点,如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
已知如图点D是△ABC的两外角平分线的交点,下列说法:
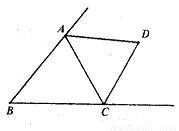
①AD=CD
②D到△ABC的三边所在直线的距离相等
③点D在∠B的平分线上
④若∠B=80°,则∠D=50°
其中正确的说法的序号是_____________________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
当k=_______时,关于x的方程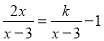 会产生增根.
会产生增根.
在解分式方程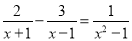 时,小兰的解法如下:
时,小兰的解法如下:
【解析】
方程两边同乘以(x+1)(x-1),得
2(x-1)-3=1. ①
2x-1-3=1. ②
解得 x=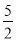 .
.
检验:x=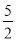 时,(x+1)(x-1) ≠0, ③
时,(x+1)(x-1) ≠0, ③
所以,原分式方程的解为x=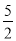 . ④
. ④
如果假设基于上一步骤正确的前提下,
你认为小兰在哪些步骤中出现了错误________(只填序号).
查看答案已知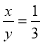 ,则
,则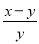 的值为_________.
的值为_________.
已知图中的两个三角形全等,则∠1等于____________。
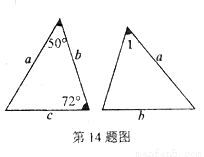
分解因式: 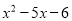 =________.
=________.
当x______时,分式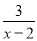 有意义.
有意义.
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.
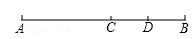
先去括号,再合并同类项:3(2x2﹣y2)﹣2(3y2﹣2x2).
查看答案化简:﹣2x2﹣5x+3﹣3x2+6x﹣1.
查看答案当a=﹣1,b=1时,求下列代数式的值.
(1)(3a+2b)(2a﹣b);
(2)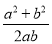 .
.
计算:
(1)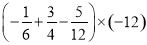 ;
;
(2)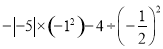 .
.
计算:2xy2﹣3xy2=__.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各组数不能作为直角三角形边长的是( )
A. 3,4,5 B. 8,15,17 C. 7,9,11 D. 9,12,15
C 【解析】A.∵ ,∴3,4,5可以作为直角三角形的边长; B.∵ ,∴8,15,17可以作为直角三角形的边长; C.∵ ,∴7,9,11可以作为直角三角形的边长; D.∵ ,∴9,12,15可以作为直角三角形的边长; 故选C.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
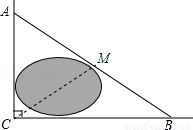
A. 0.5km B. 0.6km C. 0.9km D. 1.2km
查看答案如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
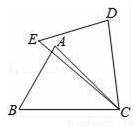
A. BC=EC,∠B=∠E B. BC=EC,AC=DC C. BC=DC,∠A=∠D D. ∠B=∠E,∠A=∠D
查看答案下列各数中,3.141 59, 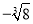 ,0.131 131 113…,-π,
,0.131 131 113…,-π, 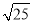 ,
, 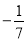 ,无理数的个数有( )
,无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案在下列“禁毒”“和平”“志愿者”“节水”这四个标志中,属于轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
从2012年4月1日起厦门市实行新的自来水收费阶梯水价,收费标准如下表所示:
月用水量 | 不超过15吨的部分 | 超过15吨不超过25吨的部分 | 超过25吨的部分 |
收费标准 (元/吨) | 2.2 | 3.3 | 4.4 |
备注:①.每月居民用水缴费包括实际用水的水费和污水处理费两部分.
②.以上表中的价格均不包括1元/吨的污水处理费
(1)某用户12月份用水量为20吨,则该用户12月份应缴水费是多少?
(2)若某用户的月用水量为m吨,请用含m的式子表示该用户月所缴水费.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

